Question

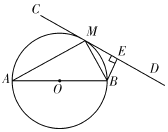
【题目】如图,AB为⊙O的直径，直线CD切⊙O于点M，BE丄CD于点E.

（1）求证:∠BME=∠MAB；

（2）求证：BM2=BEAB；

（3）若BE=，sin∠BAM=,求线段AM的长.

Answer 1

【答案】（1）见解析；（2）8

【解析】

试题

（1）如图，连接OM，由CD切⊙O于点M证得∠BME和∠OMB互余；由AB是⊙O直径证得∠AMO和∠OMB互余；从而可得∠BME=∠AMO，再证∠AMO=∠BAM即可得到结论；

（2）首先证∠BEM=∠BMA=90°，结合（1）中所得∠BME=∠BAM可证得△BEM∽△BMA，由此可得BE:BM=BM:AB，即BM2=BE·AB；

（3）由∠BME=∠BAM和sin∠BAM=，可得sin∠BME=，从而在Rt△BME中，可得BM=BE=6；然后在Rt△ABM中，由sin∠BAM=,可得AB=BM=10，最后在Rt△ABM中由勾股定理可求得AM的长.

试题解析：

（1）如图，连接OM.

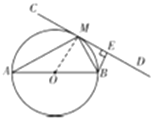
∵直线CD切⊙O于点M，

∴∠OMD=90°

∴∠BME+∠OMB=90°.

∵AB为⊙O的直径，

∴∠AMB=90°.

∴∠AMO+∠OMB=90°.

∴∠BME=∠AMO.

∵OA=OM,

∴∠MAB=∠AMO.

∴∠BMA=∠MAB.

（2）由（1）知∠BME=∠MAB.

∵BECD,

∴∠BEM=∠AMB=90°.

∴△BME∽△BAM.

∴ ，

∴BM2=BE·AB.

（3）由（1）知∠BME=∠MAB.

∵sin∠BAM=,

∴sin∠BME=.

在Rt△BEM中,BE=，

∴sin∠BAM==,

∴BM=BE=6.

在Rt△ABM中, sin∠BAM=，

∴sin∠BAM==,

∴AB=BM=10.

在Rt△ABM中，根据勾股定理，得AM=.