题目内容
 如图,△ABC中,角平分线AD、BE、CF相交于点H,过H点作HG⊥AC,垂足为G,那么∠AHE和∠CHG的大小关系为( )
如图,△ABC中,角平分线AD、BE、CF相交于点H,过H点作HG⊥AC,垂足为G,那么∠AHE和∠CHG的大小关系为( )分析:先根据AD、BE、CF为△ABC的角平分线可设∠BAD=∠CAD=x,∠ABE=∠CBE=y,∠BCF=∠ACF=z,
由三角形内角和定理可知,2x+2y+2z=180° 即x+y+z=90°在△AHB中由三角形外角的性质可知∠AHE=x+y=90°-z,同理在△CHG中,∠CHG=90°-z,故可得出结论.
由三角形内角和定理可知,2x+2y+2z=180° 即x+y+z=90°在△AHB中由三角形外角的性质可知∠AHE=x+y=90°-z,同理在△CHG中,∠CHG=90°-z,故可得出结论.
解答:解:∵AD、BE、CF为△ABC的角平分线
∴可设∠BAD=∠CAD=x,∠ABE=∠CBE=y,∠BCF=∠ACF=z,
∴2x+2y+2z=180° 即x+y+z=90°
∵在△AHB中,∠AHE=x+y=90°-z,
在△CHG中,∠CHG=90°-z,
∴∠AHE=∠CHG.
故选C.
∴可设∠BAD=∠CAD=x,∠ABE=∠CBE=y,∠BCF=∠ACF=z,
∴2x+2y+2z=180° 即x+y+z=90°
∵在△AHB中,∠AHE=x+y=90°-z,
在△CHG中,∠CHG=90°-z,
∴∠AHE=∠CHG.
故选C.
点评:本题考查的是三角形的内角和定理及三角形外角的性质,熟知三角形的内角和180°,三角形的外角等于和它不相邻的两个内角的和是解答此题的关键.

练习册系列答案
相关题目
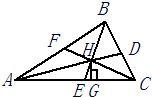 23、如图,△ABC中,角平分线AD、BE、CF相交于点H,过H点作HG⊥AC,垂足为G,那么∠AHE=∠CHG吗?为什么?
23、如图,△ABC中,角平分线AD、BE、CF相交于点H,过H点作HG⊥AC,垂足为G,那么∠AHE=∠CHG吗?为什么?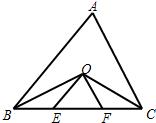 21、如图,△ABC中,角平分线BO与CO的相交点O,OE∥AB,OF∥AC,△OEF的周长=10,求BC的长.
21、如图,△ABC中,角平分线BO与CO的相交点O,OE∥AB,OF∥AC,△OEF的周长=10,求BC的长.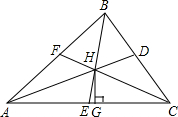 如图,△ABC中,角平分线AD、BE、CF相交于点H,过H点作HG⊥AC,垂足为G,那么∠AHE=∠CHG吗?为什么?
如图,△ABC中,角平分线AD、BE、CF相交于点H,过H点作HG⊥AC,垂足为G,那么∠AHE=∠CHG吗?为什么?