题目内容
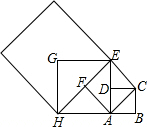 如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…,记正方形ABCD的边长a1=1,依上述方法所作的正方形的边长依次为a1,a2,a3,…,an,根据上述规律,则第n个正方形的边长an的表达式为( )
如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGH,如此下去…,记正方形ABCD的边长a1=1,依上述方法所作的正方形的边长依次为a1,a2,a3,…,an,根据上述规律,则第n个正方形的边长an的表达式为( )分析:求a2的长即AC的长,根据直角△ABC中AB2+BC2=AC2可以计算,同理计算a3、a4.由求出的a2=
a1,a3=
a2…,an=
an-1可以找出规律,得到第n个正方形边长的表达式.
| 2 |
| 2 |
| 2 |
解答:解:∵a2=AC,且在直角△ABC中,AB2+BC2=AC2,
∴a2=
a1=
,
同理a3=
a2=(
)2a1=2,
a4=
a3=(
)3a1=2
;
由此可知:
a2=
a1=
,a3=
a2=(
)2a1=2,a4=
a3=(
)3a1=2
;…
故找到规律an=(
)n-1=
.
故选D.
∴a2=
| 2 |
| 2 |
同理a3=
| 2 |
| 2 |
a4=
| 2 |
| 2 |
| 2 |
由此可知:
a2=
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
故找到规律an=(
| 2 |
| 2n-1 |
故选D.
点评:本题考查了正方形的性质,以及勾股定理在直角三角形中的运用,考查了学生找规律的能力,本题中找到an的规律是解题的关键.

练习册系列答案
相关题目
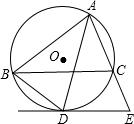 如图,已知△ABC内接于⊙O,AD平分∠BAC,交⊙O于点D,过D作⊙O的切线与AC的延长线交于点E.
如图,已知△ABC内接于⊙O,AD平分∠BAC,交⊙O于点D,过D作⊙O的切线与AC的延长线交于点E.
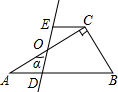 (2012•河北区一模)如图,在Rt△ABC中,∠ACB=90°,∠B=60°.点O是AC的中点,过点O的直线l从与AC重合的位置开始,绕点O作逆时针旋转,交AB边于点D.过点C作CE∥AB交直线l于点E,设直线l的旋转角为α.当α=
(2012•河北区一模)如图,在Rt△ABC中,∠ACB=90°,∠B=60°.点O是AC的中点,过点O的直线l从与AC重合的位置开始,绕点O作逆时针旋转,交AB边于点D.过点C作CE∥AB交直线l于点E,设直线l的旋转角为α.当α=