题目内容
2•(38)2•(23)2•3=2x•3y,则(x,y)=
- A.(7,17)
- B.(15,17)
- C.(7,15)
- D.(15,16)
A
分析:根据同底数幂的乘法的性质,幂的乘方的性质可得2•(38)2•(23)2•3=21•39•26•32y=27•317,再根据对应项的指数相等,即可求出x,y的值,从而求解.
解答:∵2•(38)2•(23)2•3=21•39•26•32y=27•317,
又∵2•(38)2•(23)2•3=2x•3y,
∴27•317=2x•3y,
∴x=7,y=17,
∴(x,y)=(7,17).
故选A.
点评:本题考查了同底数幂的乘法,幂的乘方,理清指数的变化是解题的关键.注意对应项的指数相等.
分析:根据同底数幂的乘法的性质,幂的乘方的性质可得2•(38)2•(23)2•3=21•39•26•32y=27•317,再根据对应项的指数相等,即可求出x,y的值,从而求解.
解答:∵2•(38)2•(23)2•3=21•39•26•32y=27•317,
又∵2•(38)2•(23)2•3=2x•3y,
∴27•317=2x•3y,
∴x=7,y=17,
∴(x,y)=(7,17).
故选A.
点评:本题考查了同底数幂的乘法,幂的乘方,理清指数的变化是解题的关键.注意对应项的指数相等.

练习册系列答案
相关题目
计算:
×(-2)2+|(-1)-2+
|+5-1的结果是( )
| 3 | -
| ||
| 3 | 8 |
A、-
| ||
| B、0 | ||
C、
| ||
D、
|
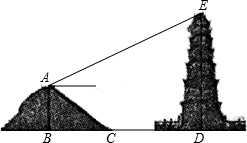 高度约为多少米?(参考数据:sin20°=0.36,cos21°=0.93,tan21°=0.38,
高度约为多少米?(参考数据:sin20°=0.36,cos21°=0.93,tan21°=0.38, 38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80 )
38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80 )