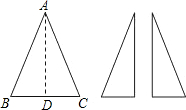题目内容
如图,已知BC为等腰三角形纸片ABC的底边,AD⊥BC,AD=BC.将此三角形纸片沿AD剪开,得到两个三角形,若把这两个三角形拼成一个平行四边形,则得到的四边形是

- A.只能是平行四边形
- B.只能为菱形
- C.只能为梯形
- D.可能是矩形
D
分析:分别以小直角三角形的三边为对角线,并令对应边重合,即可拼出图形,然后根据平行四边形的判定条件作答.对于此类问题,学生只要亲自动手操作,答案就会很直观地呈现.
解答:①将三角形ADC和三角形ABC的斜边重合,其中A与C重合,可拼成矩形;
②将三角形ADC和三角形ABC的斜边重合,其中A与A重合,可拼成一个四边形;
③将DB重合,其中D与B重合,可拼成一个平行四边形;
④将AD重合,其中A与D重合,可拼成一个平行四边形.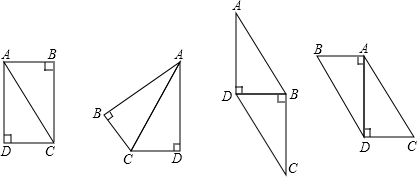
∴只有D符合要求.
故选D.
点评:本题灵活考查了平行四边形的判定,熟练掌握判定定理是解题的关键.本题一方面考查了学生的动手操作能力,另一方面考查了学生的空间想象能力,重视知识的发生过程,让学生体验学习的过程.
分析:分别以小直角三角形的三边为对角线,并令对应边重合,即可拼出图形,然后根据平行四边形的判定条件作答.对于此类问题,学生只要亲自动手操作,答案就会很直观地呈现.
解答:①将三角形ADC和三角形ABC的斜边重合,其中A与C重合,可拼成矩形;
②将三角形ADC和三角形ABC的斜边重合,其中A与A重合,可拼成一个四边形;
③将DB重合,其中D与B重合,可拼成一个平行四边形;
④将AD重合,其中A与D重合,可拼成一个平行四边形.

∴只有D符合要求.
故选D.
点评:本题灵活考查了平行四边形的判定,熟练掌握判定定理是解题的关键.本题一方面考查了学生的动手操作能力,另一方面考查了学生的空间想象能力,重视知识的发生过程,让学生体验学习的过程.

练习册系列答案
相关题目
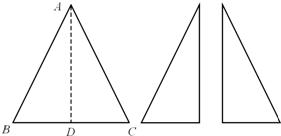
 14、如图,已知BC为等腰三角形纸片ABC的底边,AD⊥BC,∠BAC≠90度.将此三角形纸片沿AD剪开,得到两个三角形,若把这两个三角形拼成一个平行四边形,则能拼出平行四边形
14、如图,已知BC为等腰三角形纸片ABC的底边,AD⊥BC,∠BAC≠90度.将此三角形纸片沿AD剪开,得到两个三角形,若把这两个三角形拼成一个平行四边形,则能拼出平行四边形
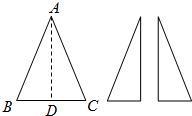
 8、如图,已知BC为等腰三角形纸片ABC的底边,AD⊥BC.将此三角形纸片沿AD剪开,得到两个三角形,若把这两个三角形拼成一个平面四边形,则能拼出( )个平行四边形.
8、如图,已知BC为等腰三角形纸片ABC的底边,AD⊥BC.将此三角形纸片沿AD剪开,得到两个三角形,若把这两个三角形拼成一个平面四边形,则能拼出( )个平行四边形.