题目内容
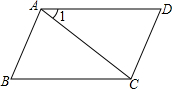如图，∠1=30°，∠B=60°，AB⊥AC，则下列说法正确的是
- A.AB∥CD
- B.AD∥BC
- C.AC⊥CD
- D.∠DAB+∠D=180°
B
分析：因为AB⊥AC，所以∠BAC=90°，又因为∠1=30°，∠B=60°，则可求得∠1=∠BCA=30°，故AD∥BC．
解答：∵AB⊥AC，
∴∠BAC=90°．
∵∠1=30°，∠B=60°，
∴∠BCA=30°．
∴∠1=∠BCA．
∴AD∥BC．
故选B．
点评：正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．
分析：因为AB⊥AC，所以∠BAC=90°，又因为∠1=30°，∠B=60°，则可求得∠1=∠BCA=30°，故AD∥BC．
解答：∵AB⊥AC，
∴∠BAC=90°．
∵∠1=30°，∠B=60°，
∴∠BCA=30°．
∴∠1=∠BCA．
∴AD∥BC．
故选B．
点评：正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．
练习册系列答案
相关题目
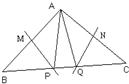18、如图，∠PAQ=30°，若MP和NQ分别垂直平分AB和AC，则∠BAC的度数是
6、如图，∠AOB=30°，∠AOB内有一定点P，且OP=10．在OA上有一点Q，OB上有一点R．若△PQR周长最小，则最小周长是（ ）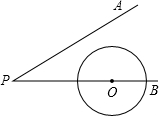
（2012•海南）如图，∠APB=30°，圆心在PB上的⊙O的半径为1cm，OP=3cm，若⊙O沿BP方向平移，当⊙O与PA相切时，圆心O平移的距离为
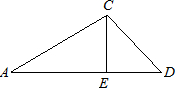如图，∠A=30°，∠D=45°，CE=2，CE⊥AD，则△ADC面积=
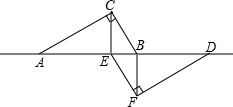如图，含30°的两块相同三角板ABC和DEF都是斜边为4cm的直角三角形，且A、E、B、D（B、E不重合）都在同一直线上，连接CE、BF．