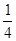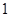题目内容
如图,请按照要求回答问题:

(1)数轴上的点C表示的数是 ______;线段AB的中点D表示的数是_____,
(2)线段AB的中点D与线段BC的中点E的距离DE等于多少?
(3)在数轴上方有一点M,下方有一点N,且∠ABM=120°,∠CBN=60°,请画出示意图,判断 BC能否平分∠MBN,并说明理由.

(1)数轴上的点C表示的数是 ______;线段AB的中点D表示的数是_____,
(2)线段AB的中点D与线段BC的中点E的距离DE等于多少?
(3)在数轴上方有一点M,下方有一点N,且∠ABM=120°,∠CBN=60°,请画出示意图,判断 BC能否平分∠MBN,并说明理由.
(1)2.5 , -2(2)2.75(3)BC平分∠MBN,理由见解析
解:(1)2.5 , -2 …………2分
(2)线段BC的中点E 表示的数是0.75 …………3分
DE=2+0.75=2.75 …………4分
(3)示意图(可以不标出角的度数)…………6分
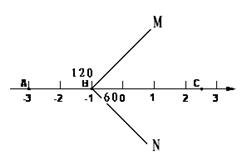
BC平分∠MBN,…………7分
理由是:
∵∠ABM=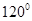
∴∠MBC=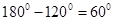
又∠CBN=60°
∴ ∠MBC= ∠CBN …………8分
即BC平分∠MBN (注:理由说清楚即可给分)
(1)观察数轴,即可知道点C表示的数;根据线段中点表示的数=这条线段的两个端点表示的数的和÷2作答;
(2)首先求出点E表示的数,然后根据数轴上两点之间的距离等于它们所表示的数的差的绝对值,即可得出DE的长;
(3)首先画出图形,然后计算出∠MBC的度数,再与∠CBN比较即可.
(2)线段BC的中点E 表示的数是0.75 …………3分
DE=2+0.75=2.75 …………4分
(3)示意图(可以不标出角的度数)…………6分

BC平分∠MBN,…………7分
理由是:
∵∠ABM=
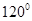
∴∠MBC=
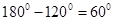
又∠CBN=60°
∴ ∠MBC= ∠CBN …………8分
即BC平分∠MBN (注:理由说清楚即可给分)
(1)观察数轴,即可知道点C表示的数;根据线段中点表示的数=这条线段的两个端点表示的数的和÷2作答;
(2)首先求出点E表示的数,然后根据数轴上两点之间的距离等于它们所表示的数的差的绝对值,即可得出DE的长;
(3)首先画出图形,然后计算出∠MBC的度数,再与∠CBN比较即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,1.5,0,
,1.5,0,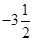 ,4,并回答问题:
,4,并回答问题: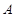 区,
区,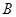 区,
区,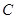 区
区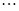
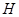 区),其中
区),其中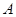 区,
区,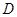 区,
区, 区各修建一栋18层的楼房;
区各修建一栋18层的楼房; 区,
区,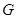 区,
区,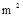 ,初步核算成本为800元/
,初步核算成本为800元/ ,初步核算成本为600元/
,初步核算成本为600元/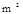 的价格销售.若房屋全部出售完,请你帮忙计算出房地产开发商的赢利预计是多少元?
的价格销售.若房屋全部出售完,请你帮忙计算出房地产开发商的赢利预计是多少元?
 =3,
=3, =7,且m-n>0,则m+n的值是( )
=7,且m-n>0,则m+n的值是( )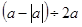 化简的结果是
化简的结果是 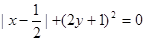 ,则
,则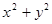 的值是( )
的值是( )