题目内容
 如图,水平放着的圆柱形排水管的截面半径是12cm,其中水面高度为6cm,求截面上有水的弓形面积.
如图,水平放着的圆柱形排水管的截面半径是12cm,其中水面高度为6cm,求截面上有水的弓形面积.分析:连接OA,OB.利用三角函数求得∠AOB的度数,然后求得扇形AOB的面积和△AOB的面积,两者的差就是阴影部分的面积.
解答: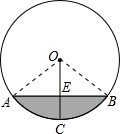 解:连接OA,OB.
解:连接OA,OB.
OE=OC-CE=12-6=6cm.
在直角△AOE中,OA=12cm,OE=6cm
∴∠OAE=30°,AE=OA•cos30°=6
cm.
∴∠AOB=2∠AOE=120°,AB=2AE=12
cm.
∴扇形AOB的面积是:
=48πcm2.
△AOB的面积是:
AB•OE=
×12
×6=36
cm2.
则阴影部分的面积是:48π-36
cm2.
 解:连接OA,OB.
解:连接OA,OB.OE=OC-CE=12-6=6cm.
在直角△AOE中,OA=12cm,OE=6cm
∴∠OAE=30°,AE=OA•cos30°=6
| 3 |
∴∠AOB=2∠AOE=120°,AB=2AE=12
| 3 |
∴扇形AOB的面积是:
| 120π×122 |
| 360 |
△AOB的面积是:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
则阴影部分的面积是:48π-36
| 3 |
点评:本题考查了扇形的面积的计算,不规则的图形的面积可以转化成规则图形的面积的和或差来计算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
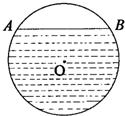 16、如图,水平放着的圆柱形排水管的截面半径是0.5m,其中水面宽AB为0.6m,则水的最大深度为
16、如图,水平放着的圆柱形排水管的截面半径是0.5m,其中水面宽AB为0.6m,则水的最大深度为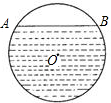 如图,水平放着的圆柱形排水管的截面为1000mm,其中水面宽AB=800mm,则水的最大深度为
如图,水平放着的圆柱形排水管的截面为1000mm,其中水面宽AB=800mm,则水的最大深度为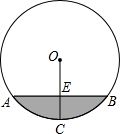 如图,水平放着的圆柱形排水管的截面半径是12cm,其中水面高度为6cm,求截面上有水的弓形面积.
如图,水平放着的圆柱形排水管的截面半径是12cm,其中水面高度为6cm,求截面上有水的弓形面积.