题目内容

已知在平行四边形ABCD中，点M、N分别是边DC、BC的中点，
AB
=
a
，
AD
=
b
，那么
MN
关于
a
、
b
的分解式是
 
．
分析：首先由点M、N分别是边DC、BC的中点，可以得到MN=
1
2
BD，又由
DB
=
AB
-
AD
，代入数值即可求得结果．
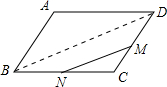解答：精英家教网解：如图：
连接BD，
∵点M、N分别是边DC、BC的中点，
∴MN=
1
2
BD，即
MN
= 
1
2
DB
，
∵
DB
=
AB
-
AD
，
又∵
AB
=
a
，
AD
=
b
，
∴
MN
=
1
2
DB
=
1
2
(
AB-
AD
)=
1
2
（
a
-
b
）=
1
2
a
-
1
2
b
．
故答案为：
1
2
a
-
1
2
b
．
点评：此题考查向量的知识．注意向量是有方向的．
练习册系列答案
相关题目
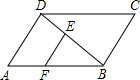精英家教网如图，已知在平行四边形ABCD中，点E、F分别在线段 BD、AB上，EF∥AD，DE：EB=2：3，EF=9，那么BC的长为
 
．
1、已知在平行四边形ABCD中，AB=14cm，BC=16cm，则此平行四边形的周长为
60
cm．
已知在平行四边形ABCD中，向量
AB
=
a
，
BC
=
b
，那么向量
BD
等于（　　）
A、
a
+
b
B、
a
-
b
C、-
a
+
b
D、-
a
-
b
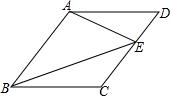精英家教网如图，已知在平行四边形ABCD中，DE：EC=2：3，
AB
=
a
，
BC
=
b
．
（1）用
a
、
b
表示
AE
、
BE
；（直接写出答案）
（2）求作
BE
分别在
BA
、
BC
方向上的分向量．（不要求写作法，但要指出图中表示结论的向量）
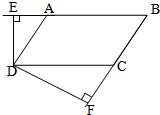18、已知在平行四边形ABCD中，DE⊥AB，DF⊥BC，∠EDF=135°，求平行四边形各角的度数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网