题目内容
 (2012•乐山)如图,直线y=2x+2与y轴交于A点,与反比例函数y=
(2012•乐山)如图,直线y=2x+2与y轴交于A点,与反比例函数y=| k |
| x |
(1)求k的值;
(2)点N(a,1)是反比例函数y=
| k |
| x |
分析:(1)根据直线解析式求A点坐标,得OA的长度;根据三角函数定义可求OH的长度,得点M的横坐标;根据点M在直线上可求点M的坐标.从而可求K的值;
(2)根据反比例函数解析式可求N点坐标;作点N关于x轴的对称点N1,连接MN1与x轴的交点就是满足条件的P点位置.
(2)根据反比例函数解析式可求N点坐标;作点N关于x轴的对称点N1,连接MN1与x轴的交点就是满足条件的P点位置.
解答:解:
(1)由y=2x+2可知A(0,2),即OA=2.…(1分)
∵tan∠AHO=2,∴OH=1.…(2分)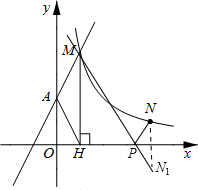
∵MH⊥x轴,∴点M的横坐标为1.
∵点M在直线y=2x+2上,
∴点M的纵坐标为4.即M(1,4).…(3分)
∵点M在y=
上,
∴k=1×4=4.…(4分)
(2)存在.
过点N作N关于x轴的对称点N1,连接MN1,交x轴于P(如图所示).此时PM+PN最小.
∵点N(a,1)在反比例函数y=
(x>0)上,
∴a=4.即点N的坐标为(4,1).…(5分)
∵N与N1关于x轴的对称,N点坐标为(4,1),
∴N1的坐标为(4,-1).…(7分)
设直线MN1的解析式为y=kx+b.
由
解得k=-
,b=
.…(9分)
∴直线MN1的解析式为y=-
x+
.
令y=0,得x=
.
∴P点坐标为(
,0).…(10分)
(1)由y=2x+2可知A(0,2),即OA=2.…(1分)
∵tan∠AHO=2,∴OH=1.…(2分)

∵MH⊥x轴,∴点M的横坐标为1.
∵点M在直线y=2x+2上,
∴点M的纵坐标为4.即M(1,4).…(3分)
∵点M在y=
| k |
| x |
∴k=1×4=4.…(4分)
(2)存在.
过点N作N关于x轴的对称点N1,连接MN1,交x轴于P(如图所示).此时PM+PN最小.
∵点N(a,1)在反比例函数y=
| 4 |
| x |
∴a=4.即点N的坐标为(4,1).…(5分)
∵N与N1关于x轴的对称,N点坐标为(4,1),
∴N1的坐标为(4,-1).…(7分)
设直线MN1的解析式为y=kx+b.
由
|
| 5 |
| 3 |
| 17 |
| 3 |
∴直线MN1的解析式为y=-
| 5 |
| 3 |
| 17 |
| 3 |
令y=0,得x=
| 17 |
| 5 |
∴P点坐标为(
| 17 |
| 5 |
点评:此题考查一次函数的综合应用,涉及线路最短问题,难度中等.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
 (2012•乐山)如图,A、B两点在数轴上表示的数分别为a、b,下列式子成立的是( )
(2012•乐山)如图,A、B两点在数轴上表示的数分别为a、b,下列式子成立的是( ) (2012•乐山)如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
(2012•乐山)如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论: (2012•乐山)如图,⊙O是四边形ABCD的内切圆,E、F、G、H是切点,点P是优弧
(2012•乐山)如图,⊙O是四边形ABCD的内切圆,E、F、G、H是切点,点P是优弧
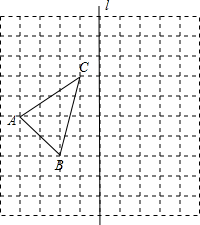 (2012•乐山)如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(2012•乐山)如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).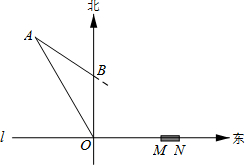 (2012•乐山)如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距
(2012•乐山)如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距