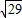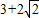题目内容
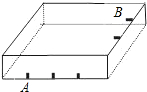
如图是一个长4m，宽3m，高2m的有盖仓库，在其内壁的A处（长的四等分）有一只壁虎，B处（宽的三等分）有一只蚊子，则壁虎爬到蚊子处最短距离为5m
5m
．分析：先把长方体的侧面展开，再连接AB，根据勾股定理求出AB的长即可．
解答：解：有两种展开方法：
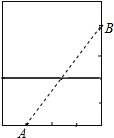
①将长方体展开成如图所示，连接A、B，
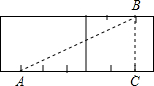
根据两点之间线段最短，AB=
=
m；
②将长方体展开成如图所示，连接A、B，则AB=
=5m，
∵5＜
，
∴壁虎爬到蚊子处最短距离为5m．
故答案为：5m．
①将长方体展开成如图所示，连接A、B，
根据两点之间线段最短，AB=
| 52+22 |
| 29 |
②将长方体展开成如图所示，连接A、B，则AB=
| 32+42 |
∵5＜
| 29 |
∴壁虎爬到蚊子处最短距离为5m．
故答案为：5m．
点评：本题考查的是平面展开-最短路线问题，根据题意画出长方体的侧面展开图是解答此题的关键．
练习册系列答案
相关题目
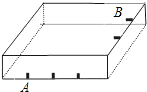如图是一个长4m，宽3m，高2m的有盖仓库，在其内壁的A处（长的四等分）有一只壁虎，B处（宽的三等分）有一只蚊子，则壁虎爬到蚊子处最短距离为（ ）m．| A、4.8 | ||
B、
| ||
| C、5 | ||
D、3+2
|
C．5
D．
