题目内容
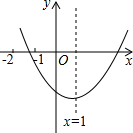 二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论中,正确结论的有( )个.
二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论中,正确结论的有( )个.①b2-4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0.
| A、1 | B、2 | C、3 | D、4 |
练习册系列答案
相关题目
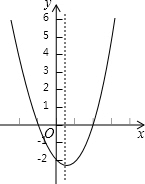 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )| A、函数有最小值 | ||
B、对称轴是直线x=
| ||
C、当x<
| ||
| D、当-1<x<2时,y>0 |
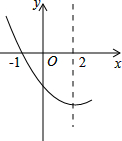 如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).有下列结论:
如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0).有下列结论:①abc>0;②4a-2b+c<0;③4a+b=0;④抛物线与x轴的另一个交点是(5,0);⑤点(-3,y1),(6,y2)都在抛物线上,则有y1<y2.
其中正确的是( )
| A、①②③ | B、②④⑤ | C、①③④ | D、③④⑤ |
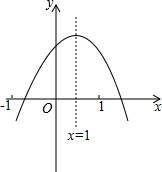 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①ac>0;
②a-b+c<0;
③当x<0时,y<0;
④9a+3b+c>0;
⑤方程ax2+bx+c=0(a≠0)有两个大于-1的实数根.
其中正确的结论有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
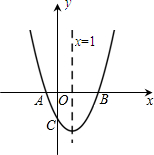 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点A坐标为(-1,0).则下面的四个结论:
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点A坐标为(-1,0).则下面的四个结论:①2a+b=0;②4a+2b+c>0;③B点坐标为(4,0);④当x<-1时,y>0.
其中正确的是( )
| A、①② | B、③④ | C、①④ | D、②③ |
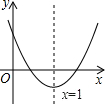 抛物线y=ax2+bx+c如图,考查下述结论:①b<0;②a-b+c>0;③b2>4ac;④2a+b<0.正确的有( )
抛物线y=ax2+bx+c如图,考查下述结论:①b<0;②a-b+c>0;③b2>4ac;④2a+b<0.正确的有( )| A、①② | B、①②③ | C、②③④ | D、①②③④ |
已知二次函数y=-x2+
x+
,当自变量x取m时对应的函数值大于0,当自变量x分别取m-1与m+1时对应的函数值为y1、y2,则y1、y2满足( )
| 1 |
| 10 |
| 1 |
| 5 |
| A、y1<0,y2<0 |
| B、y1>0,y2>0 |
| C、y1<0,y2>0 |
| D、y1>0,y2<0 |
 如图,抛物线y=-x2-4x+c(c<0)与x轴交于点A和点B(n,0),点A在点B的左侧,则AB的长是( )
如图,抛物线y=-x2-4x+c(c<0)与x轴交于点A和点B(n,0),点A在点B的左侧,则AB的长是( )| A、4-2n | B、4+2n | C、8-2n | D、8+2n |

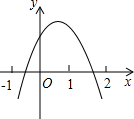 已知抛物线y=ax2+bx+c的开口向下,且经过点(1,2),与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2,下列结论:
已知抛物线y=ax2+bx+c的开口向下,且经过点(1,2),与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2,下列结论: