题目内容
【题目】求两个正整数的最大公约数是常见的数学问题,中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法——更相减损术,术曰:“可半者半之,不可半者,副置分母、子之数,以少成多,更相减损,求其等也,以等数约之.”意思是说,要求两个正整数的最大公约数,先用较大的数减去较小的数,得到差,然后用减数与差中的较大数减去较小数,以此类推,当减数与差相等时,此时的差(或减数)即为这两个正整数的最大公约数.例如:求91与56的最大公约数:
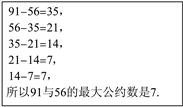
【答案】78,104,143的最大公约数是13.
【解析】
(1)根据题目,首先弄懂题意,然后根据例子写出答案,
(2)可以先求出104与78的最大公约数为26,再利用辗转除法,我们可以求出26与14的最大公约数为13,进而得到答案.
(1)108-45=63,
63-45=18,
45-18=27,
27-18=9,
18-9=9,
所以108与45的最大公约数是9.
(2)先求104与78的最大公约数:
104-78=26,
78-26=52,
52-26=26,
所以104与78的最大公约数是26,
再求26与143的最大公约数:
143-26=117,
117-26=91,
91-26=65,
65-26=39,
39-26=13,
26-13=13,
所以26与143的最大公约数是13.
所以78,104,143的最大公约数是13.

练习册系列答案
相关题目