题目内容
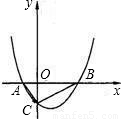
如图,己知抛物线y=x2+px+q与x轴交于A、B两点,∠ACB=90°,交y轴负半轴于C点,点B在点A的右侧,且| 1 |
| OA |
| 1 |
| OB |
| 2 |
| OC |
(1)求抛物线的解析式,
(2)求△ABC的外接圆面积;
(3)设抛物线y=x2+px+q的顶点为D,求四边形ACDB的面积;
(4)在抛物线y=x2+px+q上是否存在点P,使得△PAB的面积为2
| 2 |
 出它们的坐标;如果没有,说明理由.
出它们的坐标;如果没有,说明理由.
分析:(1)由于∠ACB=90°,所以可由射影定理和韦达定理求抛物线的解析式;
(2)求出函数与x轴的交点坐标,计算出AB的值,便可求出半径得到圆的面积;
(3)将四边形的面积转化为S△ACO+S△DEB+S梯形COED.
(4)由于底边值固定,找到高相同的三角形即可.
(2)求出函数与x轴的交点坐标,计算出AB的值,便可求出半径得到圆的面积;
(3)将四边形的面积转化为S△ACO+S△DEB+S梯形COED.
(4)由于底边值固定,找到高相同的三角形即可.
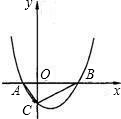
解答: 解:(1)设A点横坐标为x1、B点横坐标x2;
解:(1)设A点横坐标为x1、B点横坐标x2;
由射影定理得-x1•x2=q2①,
由韦达定理得
x1•x2=q,x1+x2=-p,
又因为
-
=
,
所以
=
②,
将x1•x2=q代入-x1•x2=q2①
得,-q=q2,解得q=-1或q=0(不合题意,舍去).
将x1•x2=q,x1+x2=-p代入
=
②
得,
=
,p=-2,于是抛物线的解析式y=x2-2x-1.
(2)令y=0,所以x2-2x-1=0,
解得x1=1-
,x2=1+
;
所以AB=x2-x1=(1+
-1+
)=2
.
∴△ABC的外接圆的半径=
∴△ABC的外接圆的面积=π(
)2=2π.
(3)因为抛物线y=x2-2x-1的顶点坐标为(1,-2),作DE⊥AB于E,
所以四边形ACDB的面积=S△ACO+S△DEB+S梯形COED=
+
+
=
+1.
(4)AB=2
,
要使△PAB的面积为2
,只需P点到x轴即AB所在直线的距离为2.
∴P点的纵坐标为2或-2,代入y=x2-2x-1得:
∴P点的坐标为(3,2),(-1,2),(1,-2).
 解:(1)设A点横坐标为x1、B点横坐标x2;
解:(1)设A点横坐标为x1、B点横坐标x2;由射影定理得-x1•x2=q2①,
由韦达定理得
x1•x2=q,x1+x2=-p,
又因为
| 1 |
| OA |
| 1 |
| OB |
| 2 |
| OC |
所以
| x1+x2 |
| x1x2 |
| 2 |
| q |
将x1•x2=q代入-x1•x2=q2①
得,-q=q2,解得q=-1或q=0(不合题意,舍去).
将x1•x2=q,x1+x2=-p代入
| x1+x2 |
| x1x2 |
| 2 |
| q |
得,
| -p |
| q |
| 2 |
| q |
(2)令y=0,所以x2-2x-1=0,
解得x1=1-
| 2 |
| 2 |
所以AB=x2-x1=(1+
| 2 |
| 2 |
| 2 |
∴△ABC的外接圆的半径=
| 2 |
∴△ABC的外接圆的面积=π(
| 2 |
(3)因为抛物线y=x2-2x-1的顶点坐标为(1,-2),作DE⊥AB于E,
所以四边形ACDB的面积=S△ACO+S△DEB+S梯形COED=
| (2+1)×1 |
| 2 |
| ||
| 2 |
1×(
| ||
| 2 |
3
| ||
| 2 |
(4)AB=2
| 2 |
要使△PAB的面积为2
| 2 |
∴P点的纵坐标为2或-2,代入y=x2-2x-1得:
∴P点的坐标为(3,2),(-1,2),(1,-2).
点评:解答此题的关键是求出二次函数解析式,然后根据二次函数的性质以及其图象上点的坐标特征解题.

练习册系列答案
相关题目
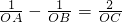 .
. ?如果有,这样的点有几个?写
?如果有,这样的点有几个?写 出它们的坐标;如果没有,说明理由.
出它们的坐标;如果没有,说明理由. .
.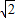 ?如果有,这样的点有几个?写出它们的坐标;如果没有,说明理由.
?如果有,这样的点有几个?写出它们的坐标;如果没有,说明理由.
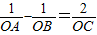 .
. ?如果有,这样的点有几个?写出它们的坐标;如果没有,说明理由.
?如果有,这样的点有几个?写出它们的坐标;如果没有,说明理由.