题目内容
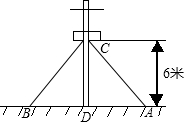 如图,在离地面高度6米的C处引拉线固定电线杆,拉线和地面成61°角,求拉线AC的长(精确到0.01米).
如图,在离地面高度6米的C处引拉线固定电线杆,拉线和地面成61°角,求拉线AC的长(精确到0.01米).
解:∵CD=6,∠CDA=90°,∠CAD=61°,
∴AC=CD÷sin61°≈6.86米.
∴拉线AC的长约为6.86米.
分析:已知CD长,∠CDA=90°,在Rt△CDA中利用61°的正弦函数值即可求得AC长.
点评:本题考查了解直角三角形的应用,此题首先把实际问题转化成直角三角形的问题,然后利用锐角三角函数正切值解决问题.
∴AC=CD÷sin61°≈6.86米.
∴拉线AC的长约为6.86米.
分析:已知CD长,∠CDA=90°,在Rt△CDA中利用61°的正弦函数值即可求得AC长.
点评:本题考查了解直角三角形的应用,此题首先把实际问题转化成直角三角形的问题,然后利用锐角三角函数正切值解决问题.

练习册系列答案
相关题目
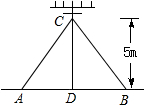 如图,在离地面高度5m处引拉线固定电线杆,拉线和地面成60°角,则拉线AC的长是( )
如图,在离地面高度5m处引拉线固定电线杆,拉线和地面成60°角,则拉线AC的长是( )| A、10m | ||||
B、
| ||||
C、
| ||||
D、5
|
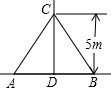 如图,在离地面高度为5m的C处引拉线固定电线杆,拉线与地面成α角,则拉线AC的长为
如图,在离地面高度为5m的C处引拉线固定电线杆,拉线与地面成α角,则拉线AC的长为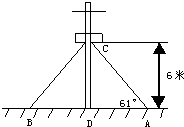 23、如图,在离地面高度6米的C处引拉线固定电线杆,拉线和地面成61°角,求拉线AC的长(精确到0.01米).
23、如图,在离地面高度6米的C处引拉线固定电线杆,拉线和地面成61°角,求拉线AC的长(精确到0.01米).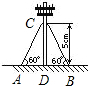 如图,在离地面高度5米处引拉线固定电线杆,拉线和地面成60°角,求拉线AC的长以及拉线下端点A与杆底D的距离AD(不取近似值).
如图,在离地面高度5米处引拉线固定电线杆,拉线和地面成60°角,求拉线AC的长以及拉线下端点A与杆底D的距离AD(不取近似值).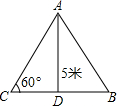 如图,在离地面高度5米处引拉线固定电线杆,拉线和地面成60°,则拉线AC的长为( )
如图,在离地面高度5米处引拉线固定电线杆,拉线和地面成60°,则拉线AC的长为( )