题目内容
已知整数满足6<m<20,如果关于x的一元二次方程mx2-(2m-1)x+m-2=0有有理根,求m的值及方程的根。
解:∵原方程有实数根
∴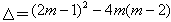 ≥0
≥0
∴m≥-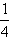 ①
①
∵原方程有有理根
∴判别式△是完全平方数
即4m+1是完全平方数
∴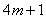 =1或4或9或16…
=1或4或9或16…
∴m=0或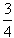 或2或
或2或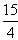 ②
②
又∵6<m<20 ③
且m为整数 ④
由①②③④知:m=12
当m=12时,原方程为: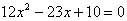
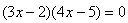
x1=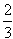 ,x2=
,x2=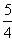
∴∴当m=12时,原方程有有理根,此时方程的根为x1=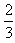 ,x2=
,x2=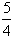 。
。
∴
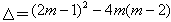 ≥0
≥0∴m≥-
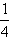 ①
①∵原方程有有理根
∴判别式△是完全平方数
即4m+1是完全平方数
∴
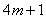 =1或4或9或16…
=1或4或9或16…∴m=0或
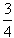 或2或
或2或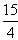 ②
②又∵6<m<20 ③
且m为整数 ④
由①②③④知:m=12
当m=12时,原方程为:
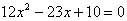
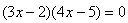
x1=
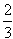 ,x2=
,x2=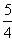
∴∴当m=12时,原方程有有理根,此时方程的根为x1=
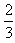 ,x2=
,x2=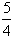 。
。
练习册系列答案
相关题目
某精品水果超市销售一种进口水果A,从去年1至7月,这种水果的进价一路攀升,每千克A的进价 与月份
与月份 (
( ,且
,且 为整数),之间的函数关系式如下表 :
为整数),之间的函数关系式如下表 :
随着我国对一些国家进出口关税的调整,该水果的进价涨势趋缓,在8至12月份每千克水果A的进价 与月份
与月份 (
( ,且
,且 为整数)之间存在如下图所示的变化趋势.
为整数)之间存在如下图所示的变化趋势.
(1)请观察表格和图像,用所学过的一次函数、反比例函数、二次函数的有关知识分别写出 与
与 和
和 与
与 的函数关系式.
的函数关系式.
(2)若去年该水果的售价为每千克180元,且销售该水果每月必须支出(除进价外)的固定支出为300元,已知该水果在1月至7月的销量 (千克)与月份
(千克)与月份 满足:
满足: ;8月至12月的销量
;8月至12月的销量 (千克)与月份
(千克)与月份 满足:
满足: ;则该水果在第几月销售时,可使该月所获得的利润最大?并求出此时的最大利润.
;则该水果在第几月销售时,可使该月所获得的利润最大?并求出此时的最大利润.
(3)今年1月到6月,该进口水果的进价进行调整,每月进价均比去年12月的进价上涨15元,且每月的固定支出(除进价外)增加了15%,已知该进口水果的售价在去年的基础上提高了 (
( <100),与此同时每月的销量均在去年12月的基础上减少了
<100),与此同时每月的销量均在去年12月的基础上减少了 ,这样销售下去要使今年1至6月的总利润为68130元,试求出
,这样销售下去要使今年1至6月的总利润为68130元,试求出 的值.(保留两个有效数字)(参考数据:
的值.(保留两个有效数字)(参考数据:
 ,
, ,
, )
)
 与月份
与月份 (
( ,且
,且 为整数),之间的函数关系式如下表 :
为整数),之间的函数关系式如下表 :月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
 (元/千克) (元/千克) | 50 | 60 | 70 | 80 | 90 | 100 | 110 |
 与月份
与月份 (
( ,且
,且 为整数)之间存在如下图所示的变化趋势.
为整数)之间存在如下图所示的变化趋势.(1)请观察表格和图像,用所学过的一次函数、反比例函数、二次函数的有关知识分别写出
 与
与 和
和 与
与 的函数关系式.
的函数关系式.(2)若去年该水果的售价为每千克180元,且销售该水果每月必须支出(除进价外)的固定支出为300元,已知该水果在1月至7月的销量
 (千克)与月份
(千克)与月份 满足:
满足: ;8月至12月的销量
;8月至12月的销量 (千克)与月份
(千克)与月份 满足:
满足: ;则该水果在第几月销售时,可使该月所获得的利润最大?并求出此时的最大利润.
;则该水果在第几月销售时,可使该月所获得的利润最大?并求出此时的最大利润.(3)今年1月到6月,该进口水果的进价进行调整,每月进价均比去年12月的进价上涨15元,且每月的固定支出(除进价外)增加了15%,已知该进口水果的售价在去年的基础上提高了
 (
( <100),与此同时每月的销量均在去年12月的基础上减少了
<100),与此同时每月的销量均在去年12月的基础上减少了 ,这样销售下去要使今年1至6月的总利润为68130元,试求出
,这样销售下去要使今年1至6月的总利润为68130元,试求出 的值.(保留两个有效数字)(参考数据:
的值.(保留两个有效数字)(参考数据:
 ,
, ,
, )
)
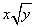 +
+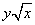 -
-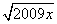 -
-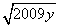 +
+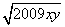 =2009,则
=2009,则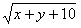 =( )。
=( )。