题目内容
若关于x的分式方程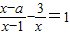 有正数解,则a的取值范围是 .
有正数解,则a的取值范围是 .
【答案】分析:先解关于x的分式方程,求得x的值,然后再依据“解是正数”建立不等式求a的取值范围.
解答:解:去分母,得x(x-a)-3(x-1)=x(x-1)
解得:x=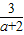 .
.
∵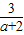 >0
>0
∴a+2>0,
∴a>-2,且x≠1,
∴a≠1
∴a>-2且a≠1.
点评:由于我们的目的是求a的取值范围,因此也没有必要求得x的值,求得3x=2-a即可列出关于a的不等式了,另外,解答本题时,易漏掉a≠-4,这是因为忽略了x-2≠0这个隐含的条件而造成的,这应引起同学们的足够重视.
解答:解:去分母,得x(x-a)-3(x-1)=x(x-1)
解得:x=
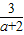 .
.∵
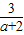 >0
>0∴a+2>0,
∴a>-2,且x≠1,
∴a≠1
∴a>-2且a≠1.
点评:由于我们的目的是求a的取值范围,因此也没有必要求得x的值,求得3x=2-a即可列出关于a的不等式了,另外,解答本题时,易漏掉a≠-4,这是因为忽略了x-2≠0这个隐含的条件而造成的,这应引起同学们的足够重视.

练习册系列答案
相关题目
 有增根,则
有增根,则
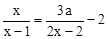 有非负数解,则a的取值范围是 .
有非负数解,则a的取值范围是 .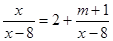 有增根,则
有增根,则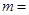
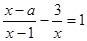 有增根,则
有增根,则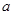 = .
= .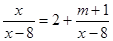 有增根,则
有增根,则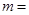 .
.