题目内容
【题目】如图,一个3×2的矩形(即长为3,宽为2)可以用两种不同的方式分割成3或6个边长是正整数的小正方形,即:小正方形的个数最多是6个,最少是3个.
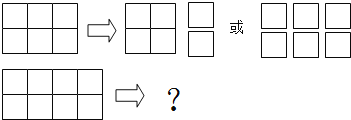
(1)一个5×2的矩形用不同的方式分割后,小正方形的个数最多是 个,最少是 个;
(2)一个7×2的矩形用不同的方式分割后,小正方形的个数最多是 个,最少是 个;
(3)一个(2n+1)×2的矩形用不同的方式分割后,小正方形的个数最多是 个,最少是 个.(n是正整数)
【答案】(1)4;10;(2)5;14;(3)4n+2;n+2.
【解析】
试题分析:(1)一个5×2的矩形最少可分成4个正方形,最多可分成10个正方形;
(2)一个7×2的矩形最少可分成5个正方形,最多可分成14个正方形;
(3)根据上述结果找出其中的规律,然后用含字母n的式子表示这一规律即可.
试题解析:(1)一个5×2的矩形最少可分成4个正方形,最多可分成10个正方形;
(2)一个7×2的矩形最少可分成5个正方形,最多可分成14个正方形;
(3)第一个图形:是一个3×2的矩形,最少可分成1+2个正方形,最多可分成1×4+2个正方形;
第二个图形:是一个5×2的矩形,最少可分成2+2个正方形,最多可分成2×4+2个正方形;
第三个图形:是一个7×2的矩形,最少可分成3+2个正方形,最多可分成3×4+2个正方形;
…
第n个图形:是一个(2n+1)×2的矩形,最多可分成n×4+2=4n+2个正方形,最少可分成n+2个正方形.

练习册系列答案
相关题目