题目内容
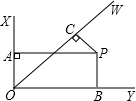 如图,∠XOY=90°,OW平分∠XOY,PA⊥OX,PB⊥OY,PC⊥OW,其中A,B,C为垂足,若OA+OB+OC=1,则OC=
如图,∠XOY=90°,OW平分∠XOY,PA⊥OX,PB⊥OY,PC⊥OW,其中A,B,C为垂足,若OA+OB+OC=1,则OC=
- A.
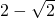
- B.
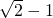
- C.
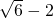
- D.

B
分析:先过AP与OW的交点作EF⊥OB,根据已知条件得出∠AEO=∠CEP=45°,再根据sin45°=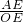 =
=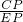 =
= ,表示出个边的值,再进行相加,即可得出答案.
,表示出个边的值,再进行相加,即可得出答案.
解答:过AP与OW的交点作EF⊥OB,
∵∠XOY=90°,OW平分∠XOY,
∴∠AOC=∠COB=45°,
∴∠AEO=∠CEP=45°,
∴sin45°=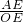 =
=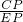 =
= ,
,
AE= OE,EP=
OE,EP= CP,OF=
CP,OF= EF,
EF,
∵cos45°=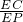 ,
,
∴EC= EP,
EP,
∵AO=EF,OF+EP=OB,OC=OE+EC,
∴OC= -1;
-1;
故答案为:B.

点评:此题考查了等腰直角三角形,用到的知识点是特殊角的三角函数值,解题的关键是根据角的度数表示出各个边.
分析:先过AP与OW的交点作EF⊥OB,根据已知条件得出∠AEO=∠CEP=45°,再根据sin45°=
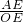 =
=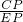 =
= ,表示出个边的值,再进行相加,即可得出答案.
,表示出个边的值,再进行相加,即可得出答案.解答:过AP与OW的交点作EF⊥OB,
∵∠XOY=90°,OW平分∠XOY,
∴∠AOC=∠COB=45°,
∴∠AEO=∠CEP=45°,
∴sin45°=
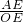 =
=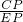 =
= ,
,AE=
 OE,EP=
OE,EP= CP,OF=
CP,OF= EF,
EF,∵cos45°=
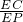 ,
,∴EC=
 EP,
EP,∵AO=EF,OF+EP=OB,OC=OE+EC,
∴OC=
 -1;
-1;故答案为:B.

点评:此题考查了等腰直角三角形,用到的知识点是特殊角的三角函数值,解题的关键是根据角的度数表示出各个边.

练习册系列答案
相关题目
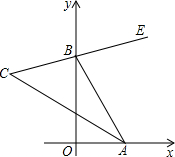 已知,如图,∠XOY=90°,点A、B分别在射线OX、OY上移动,BE是∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.
已知,如图,∠XOY=90°,点A、B分别在射线OX、OY上移动,BE是∠ABY的平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围. 如图,∠XOY=90°,OW平分∠XOY,PA⊥OX,PB⊥OY,PC⊥OW,其中A,B,C为垂足,若OA+OB+OC=1,则OC=( )
如图,∠XOY=90°,OW平分∠XOY,PA⊥OX,PB⊥OY,PC⊥OW,其中A,B,C为垂足,若OA+OB+OC=1,则OC=( ) 如图,∠XOY=90°,OW平分∠XOY,PA⊥OX,PB⊥OY,PC⊥OW,其中A,B,C为垂足,若OA+OB+OC=1
如图,∠XOY=90°,OW平分∠XOY,PA⊥OX,PB⊥OY,PC⊥OW,其中A,B,C为垂足,若OA+OB+OC=1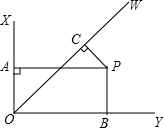 如图,∠XOY=90°,OW平分∠XOY,PA⊥OX,PB⊥OY,PC⊥OW,其中A,B,C为垂足,若OA+OB+OC=1
如图,∠XOY=90°,OW平分∠XOY,PA⊥OX,PB⊥OY,PC⊥OW,其中A,B,C为垂足,若OA+OB+OC=1