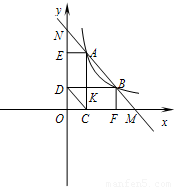题目内容
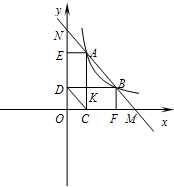 如图,直线MN分别与x轴、y轴交于点M,N,与反比例函数y=
如图,直线MN分别与x轴、y轴交于点M,N,与反比例函数y=| k |
| x |
(1)比较大小:S四边形AEOC
(2)求证:
| AK |
| BK |
| CK |
| DK |
(3)试判断AN与BM有怎样的数量关系,并说明理由.
分析:(1)从双曲线上的任一点向两坐标轴作垂线,与坐标轴所围成的矩形的面积相等;
(2)利用上题得到的结论,可以得到四边形AEDK的面积等于四边形CFBK的面积,从而得到其邻边的成绩相等,进而证得比例式成立;
(3)利用上题证得的比例式加上AKB=∠CKD可以证得△AKB∽△CKD,从而可以得到∠ABK=∠CDK,证得四边形ACDN是平行四边形后结论得证.
(2)利用上题得到的结论,可以得到四边形AEDK的面积等于四边形CFBK的面积,从而得到其邻边的成绩相等,进而证得比例式成立;
(3)利用上题证得的比例式加上AKB=∠CKD可以证得△AKB∽△CKD,从而可以得到∠ABK=∠CDK,证得四边形ACDN是平行四边形后结论得证.
解答: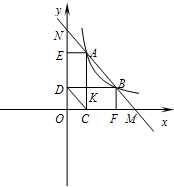 解:(1)S矩形AEOC=S矩形BDOF.
解:(1)S矩形AEOC=S矩形BDOF.
(2)∵S四边形AEDK=S矩形AEOC-S矩形DOCK,
S四边形CFBK=S矩形BDOF-S矩形DOCK.
∴S四边形AEDK=S四边形CFBK
∴AK•DK=BK•CK.
∴
=
.
(3)∵
=
,∠AKB=∠CKD=90°,
∴△AKB∽△CKD.
∴∠ABK=∠CDK,
∴AB∥CD.
∵AC∥y轴,
∴四边形ACDN是平行四边形.
∴AN=CD.
同理BM=CD.
∴AN=BM.
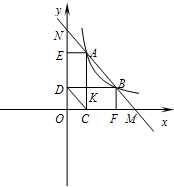 解:(1)S矩形AEOC=S矩形BDOF.
解:(1)S矩形AEOC=S矩形BDOF.(2)∵S四边形AEDK=S矩形AEOC-S矩形DOCK,
S四边形CFBK=S矩形BDOF-S矩形DOCK.
∴S四边形AEDK=S四边形CFBK
∴AK•DK=BK•CK.
∴
| AK |
| BK |
| CK |
| DK |
(3)∵
| AK |
| BK |
| CK |
| DK |
∴△AKB∽△CKD.
∴∠ABK=∠CDK,
∴AB∥CD.
∵AC∥y轴,
∴四边形ACDN是平行四边形.
∴AN=CD.
同理BM=CD.
∴AN=BM.
点评:本题是一道反比例函数的综合题,题目中还考查了比例式的证明及相似三角形的判定的知识,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,直线MN分别与x轴、y轴交于点M,N,与反比例函数y=
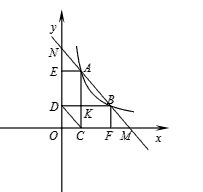
如图,直线MN分别与x轴、y轴交于点M,N,与反比例函数y= (x>0)的图象相交于点A,B.过点A分别作AC⊥x轴,AE⊥y轴,垂足分别为C,E;过点B分别作BF⊥x轴,BD⊥y轴,垂足分别为F,D,AC与BD交于点K,连接CD.
(x>0)的图象相交于点A,B.过点A分别作AC⊥x轴,AE⊥y轴,垂足分别为C,E;过点B分别作BF⊥x轴,BD⊥y轴,垂足分别为F,D,AC与BD交于点K,连接CD.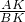 =
=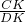 ;
;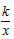 (x>0)的图象相交于点A,B.过点A分别作AC⊥x轴,AE⊥y轴,垂足分别为C,E;过点B分别作BF⊥x轴,BD⊥y轴,垂足分别为F,D,AC与BD交于点K,连接CD。
(x>0)的图象相交于点A,B.过点A分别作AC⊥x轴,AE⊥y轴,垂足分别为C,E;过点B分别作BF⊥x轴,BD⊥y轴,垂足分别为F,D,AC与BD交于点K,连接CD。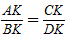 ;
;
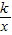 (x>0)的图象相交于点A,B.过点A分别作AC⊥x轴,AE⊥y轴,垂足分别为C,E;过点B分别作BF⊥x轴,BD⊥y轴,垂足分别为F,D,AC与BD交于点K,连接CD.
(x>0)的图象相交于点A,B.过点A分别作AC⊥x轴,AE⊥y轴,垂足分别为C,E;过点B分别作BF⊥x轴,BD⊥y轴,垂足分别为F,D,AC与BD交于点K,连接CD.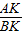 =
=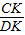 ;
;