题目内容
学校为了美化校园环境,在一块长40 m、宽20 m的长方形空地上计划新建一块长9 m、宽7 m的长方形花圃.
(1)若请你在这块空地上设计一个长方形花圃,使它的面积比学校计划新建的长方形花圃的面积多1 m2,请你给出你认为合适的三种不同的方案.
(2)在学校计划新建的长方形花圃周长不变的情况下,长方形花圃的面积能否增加2 m2 ?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由.
答案:
解析:
解析:
|
(1)方案1:长为 方案2:长为9 m,宽为 方案3:长=宽=8 m(本题的方案有无穷多种); (2)在长方形花圃周长不变的情况下,长方形花圃面积不能增加2 m2.由题意得长方形长与宽的和为16 m.设长方形花圃的长为x m,则宽为(16-x)m 解法一:x(16-x)=63+2,x2-16x+65=0,∵Δ=(-16)2-4×1×65=-4<0,∴此方程无解,∴在周长不变的情况下,长方形花圃的面积不能增加2 m2. 解法二:S长方形=x(16-x)=-x2+16x=-(x-8)2+64,∴在长方形花圃周长不变的情况下,长方形的最大面积为64 m2,因此不能增加2 m2. |

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 米,宽
米,宽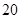 米的长方形空地上计划新建一块长
米的长方形空地上计划新建一块长 米,宽
米,宽 米的长方形花圃.
米的长方形花圃. 平方米,请你给出你认为合适的三种不同的方案;
平方米,请你给出你认为合适的三种不同的方案;
 平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由.
平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由. 米,宽
米,宽 米的长方形空地上计划新建一块长
米的长方形空地上计划新建一块长 米,宽
米,宽 米的长方形花圃.
米的长方形花圃. 平方米,请你给出你认为合适的三种不同的方案;
平方米,请你给出你认为合适的三种不同的方案;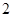
 平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由.
平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由. 米,宽
米,宽 米的长方形空地上计划新建一块长
米的长方形空地上计划新建一块长 米,宽
米,宽 米的长方形花圃.
米的长方形花圃. 平方米,请你给出你认为合适的三种不同的方案;
平方米,请你给出你认为合适的三种不同的方案; 平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由.
平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由.