题目内容
在同一直角坐标系内,二次函数y1=ax2+bx+c与y2=cx2+bx+a的图象大致为
- A.
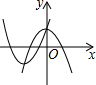
- B.
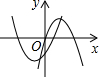
- C.
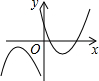
- D.
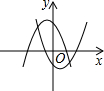
D
分析:先分析二次函数y=ax2+bx+c,得到a、c的取值范围后,对照二次函数y=cx2+bx+a的相关性质是否一致,可得答案.
解答:A、∵当二次函数y1=ax2+bx+c的图象的开口方向是向下,
∴a<0,
∴二次函数y2=cx2+bx+a与y轴交于负半轴;
故本选项错误;
B、∵当二次函数y1=ax2+bx+c的图象的开口方向是向下,
∴a<0;
又对称轴x=- >0,
>0,
∴b>0,
而该函数与y轴交于负半轴,
∴c=0;
∴二次函数y2=cx2+bx+a变为一次函数,故本选项错误;
C、∵当二次函数y1=ax2+bx+c的图象的开口方向是向上,
∴a>0,
∴二次函数y2=cx2+bx+a与y轴交于正半轴;
故本选项错误;
D、∵当二次函数y1=ax2+bx+c的图象的开口方向是向上,
∴a>0,此时c<0,
∴二次函数y2=cx2+bx+a与y轴交于正半轴;
故本选项正确.
故选D.
点评:此题主要考查了图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换.
分析:先分析二次函数y=ax2+bx+c,得到a、c的取值范围后,对照二次函数y=cx2+bx+a的相关性质是否一致,可得答案.
解答:A、∵当二次函数y1=ax2+bx+c的图象的开口方向是向下,
∴a<0,
∴二次函数y2=cx2+bx+a与y轴交于负半轴;
故本选项错误;
B、∵当二次函数y1=ax2+bx+c的图象的开口方向是向下,
∴a<0;
又对称轴x=-
 >0,
>0,∴b>0,
而该函数与y轴交于负半轴,
∴c=0;
∴二次函数y2=cx2+bx+a变为一次函数,故本选项错误;
C、∵当二次函数y1=ax2+bx+c的图象的开口方向是向上,
∴a>0,
∴二次函数y2=cx2+bx+a与y轴交于正半轴;
故本选项错误;
D、∵当二次函数y1=ax2+bx+c的图象的开口方向是向上,
∴a>0,此时c<0,
∴二次函数y2=cx2+bx+a与y轴交于正半轴;
故本选项正确.
故选D.
点评:此题主要考查了图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目