题目内容
28、(1)如图,EF⊥GF于F.∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.

(2)已知:如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.
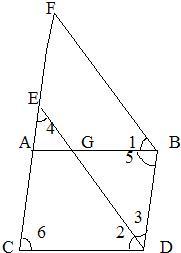

(2)已知:如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.

分析:(1)需要作辅助线,构造“三线八角”图形.可延长MF交CD于点H,利用平行线的判定证明.
(2)根据图形分析,欲证ED∥FB,需证∠5+∠1+∠3=180°.而∠6+∠2+∠4=180°,通过代换即可得出结论.
(2)根据图形分析,欲证ED∥FB,需证∠5+∠1+∠3=180°.而∠6+∠2+∠4=180°,通过代换即可得出结论.
解答:解: (1)延长MF交CD于点H.那么∠1就是△FGH的一个外角.
(1)延长MF交CD于点H.那么∠1就是△FGH的一个外角.
∵三角形的任一外角等于和它不相邻的两个内角之和,
∴∠CHF=140°-90°=50°=∠2,
∴AB∥CD.
证明:(2)∵∠3=∠4,
∴CF∥BD.(内错角相等,两直线平行)
∴∠6+∠2+∠3=180°(两直线平行,同旁内角互补),
∵∠5=∠6,∠1=∠2,
∴∠6+∠2+∠3=∠5+∠1+∠3=180°.(等量代换)
∴ED∥FB.(同旁内角互补,两直线平行)
 (1)延长MF交CD于点H.那么∠1就是△FGH的一个外角.
(1)延长MF交CD于点H.那么∠1就是△FGH的一个外角.∵三角形的任一外角等于和它不相邻的两个内角之和,
∴∠CHF=140°-90°=50°=∠2,
∴AB∥CD.
证明:(2)∵∠3=∠4,
∴CF∥BD.(内错角相等,两直线平行)
∴∠6+∠2+∠3=180°(两直线平行,同旁内角互补),
∵∠5=∠6,∠1=∠2,
∴∠6+∠2+∠3=∠5+∠1+∠3=180°.(等量代换)
∴ED∥FB.(同旁内角互补,两直线平行)
点评:此题主要考查了平行线的判定.即
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行.
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
 16、如图,EF是△ABC的中位线,将△AEF沿AB方向平移到△EBD的位置,点D在BC上,已知△AEF的面积为5,则图中阴影部分的面积为
16、如图,EF是△ABC的中位线,将△AEF沿AB方向平移到△EBD的位置,点D在BC上,已知△AEF的面积为5,则图中阴影部分的面积为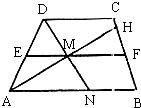 3、如图,EF为梯形ABCD的中位线,AH平分∠DAB交EF于M,延长DM交AB于N.
3、如图,EF为梯形ABCD的中位线,AH平分∠DAB交EF于M,延长DM交AB于N.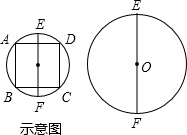 (1)如图,EF是⊙O的直径,请仅用尺规作出该圆的内接正方形ABCD,要求所作正方形的一组对边AD、BC垂直于EF.(见示意图;不写作法,但须保留作图痕迹);
(1)如图,EF是⊙O的直径,请仅用尺规作出该圆的内接正方形ABCD,要求所作正方形的一组对边AD、BC垂直于EF.(见示意图;不写作法,但须保留作图痕迹);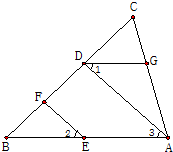 24、如图,EF∥AD,∠1=∠2,∠BAC=65°.将下面求∠AGD的过程填写完整.
24、如图,EF∥AD,∠1=∠2,∠BAC=65°.将下面求∠AGD的过程填写完整. 已知:如图,EF∥BC,点F,点C在AD上,BC=EF,AC=DF.
已知:如图,EF∥BC,点F,点C在AD上,BC=EF,AC=DF.