题目内容
【题目】如图,△ABC的角平分线相交于P,∠A=m°,
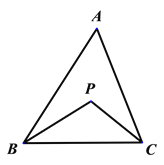
(1)若∠A=40°,求∠BPC的度数;
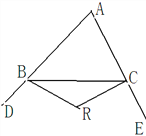
(2)设△ABC的外角∠CBD、∠BCE的平分线相交于Q, 且∠A=m°,求∠BQC的度数

(3)设△ABC的外角∠CBD、∠BCE的n等分线相交于R,且∠A=m°,∠CBR=![]() ∠CBD,∠BCR=
∠CBD,∠BCR=![]() ∠BCE,求∠BRC的度数
∠BCE,求∠BRC的度数
【答案】(1)110°
(2)90°+![]() m°
m°
(3)![]() ×180°-
×180°-![]() (此结果形式可以不同,只要正确皆可)
(此结果形式可以不同,只要正确皆可)
【解析】试题分析:(1)根据三角形内角和定理和角平分线的性质解答即可;
(2)(3)根据三角形内角和定理和三角形外角的性质解答即可.
试题解析:解:(1)∵∠A=40°,∴∠ABC+∠ACB=180°-40°=140°.∵BP、CP是角平分线,∴∠ABC=2∠PBC,∠ACB=2∠PCB,∴∠PBC+∠PCB=![]() (∠ABC+∠ACB)==
(∠ABC+∠ACB)==![]() ×140°=70°,∴∠P=180°-70°=110°.
×140°=70°,∴∠P=180°-70°=110°.
(2)∵∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,∴∠DBC+∠BCD=2∠A+∠ABC+∠ACB=∠A+180°=m+180°.∵BQ,CQ是角平分线,∴∠DBC=2∠QBC,∠BCE=2∠BCQ,∴∠QBC+∠BCQ=![]() (∠DBC+∠ECB)=
(∠DBC+∠ECB)=![]() (m+180°)=90°+
(m+180°)=90°+![]() m.在△BCQ中,∠Q=180°-(∠QBC+∠BCQ)=180°-(90°+
m.在△BCQ中,∠Q=180°-(∠QBC+∠BCQ)=180°-(90°+![]() m)=90°-
m)=90°-![]() m.
m.
(3)由(2)得:∠DBC+∠BCD=m+180°,∠RBC+∠BCR=![]() (∠DBC+∠ECB)=
(∠DBC+∠ECB)=![]() (m+180°).在△BCR中,∠R=180°-(∠RBC+∠BCR)=180°-
(m+180°).在△BCR中,∠R=180°-(∠RBC+∠BCR)=180°-![]() (m+180°)=
(m+180°)=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目