题目内容
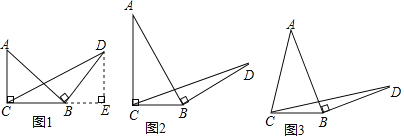
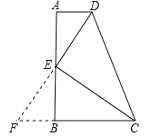
【题目】如图,四边形ABCD中,∠A = ∠B = 90°,AB边上有一点E,CE,DE分别是∠BCD和∠ADC 的角平分线,如果ABCD的面积是12,CD = 8,那么AB的长度为_____.

【答案】3
【解析】
根据角平分线的定义求出∠ADE=∠CDE,∠DCE=BCE,求出∠DCE+∠CDE=90°,延长DE交CB的延长线于点F,求出△CDF是等腰三角形;求出DE=FE,根据全等三角形的判定得出△BEF≌△AED,得到AD=BF,故FC=AD+BC=CD,再根据等腰梯形的面积公式即可求解AB的长.
∵∠A = ∠B = 90°
∴AD∥BC,∠ADC+∠BCD=180
∵ED平分∠ADC,EC平分∠BCD,
∴∠ADE=∠CDE,∠DCE=BCE
∴∠DCE+∠CDE=90
∴DE⊥EC,
延长DE交CB的延长线于点F,
∵AD∥BC,DE是∠ADC的角平分线,
∴∠CDF=∠ADE=∠DFC,
∴CD=CF,
∴△CDF是等腰三角形;
∵DE⊥EC,
∴DE=FE,
在△BEF和△AED中
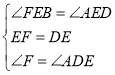
∴△BEF≌△AED(ASA),
∴AD=BF,
故FC=AD+BC=CD=8,
∵等腰梯形的面积为![]() (AD+BC)×AB=12
(AD+BC)×AB=12
即![]() ×8×AB=12
×8×AB=12
故AB=3.
故填:3.

【题目】以下关于x的各个多项式中,a,b,c,m,n均为常数.
(1)根据计算结果填写下表:
二次项系数 | 一次项系数 | 常数项 | |
(2x + l)(x + 2) | 2 | 2 | |
(2x + 1)(3x - 2) | 6 | -2 | |
(ax + b)( mx + n) | am | bn |
(2)已知(x+ 3)2(x + mx +n)既不含二次项,也不含一次项,求m + n的值.
(3) 多项式M与多项式x2-3x + 1的乘积为2x4+ ax3 + bx2+ cx -3,则2 a +b + c的值为