题目内容
设Rt△ABC的周长为p(cm),面积为s(cm2),如果p、s为整数且p=s.那么△ABC三边的长度(cm)分别为分析:设三角形三边分别是a、b、c,c为斜边,则根据勾股定理和该三角形周长和面积相等的性质可以列出方程式,根据方程式可以得到a、b的关系,根据题目中给出的a、b均为整数即可解题.
解答:解:设Rt△三边长分别为a、b、c,其中c为斜边,
由题意得a2+b2=c2①
a+b+c=
ab ②
由②得c=
ab-a-b,代入①并化简得a=4+
.
因为a、b都是正整数,所以b-4能整除8,且b≥1,
所以b只能取5、6、8、12,
则a的取值为12、8、6、5,
c的取值为13、10、10、13,
故得5、12、13或6、8、10.
由题意得a2+b2=c2①
a+b+c=
| 1 |
| 2 |
由②得c=
| 1 |
| 2 |
| 8 |
| b-4 |
因为a、b都是正整数,所以b-4能整除8,且b≥1,
所以b只能取5、6、8、12,
则a的取值为12、8、6、5,
c的取值为13、10、10、13,
故得5、12、13或6、8、10.
点评:本题考查了勾股定理在直角三角形中的运用,考查了分类讨论思想,本题中找到周长与面积相等并化简出a=4+
是解题的关键.
| 8 |
| b-4 |

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
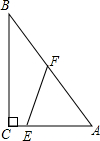 在Rt△ABC中,∠C=90°,AC=3,BC=4,点E在直角边AC上(点E与A、C两点均不重合),点F在斜边AB上(点F与A、B两点均不重合).
在Rt△ABC中,∠C=90°,AC=3,BC=4,点E在直角边AC上(点E与A、C两点均不重合),点F在斜边AB上(点F与A、B两点均不重合). (2013•河西区一模)如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E在AC上(点E与A、C都不重合),点F在斜边AB上(点F与A、B都不重合).
(2013•河西区一模)如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E在AC上(点E与A、C都不重合),点F在斜边AB上(点F与A、B都不重合).