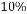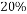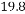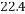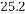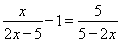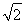Question

△ABC中，AB=AC,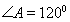，AB的中垂线交AB于D，交CA延长线于E，求证：DE=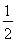BC.

 

Answer 1

证明见解析．

【解析】

试题分析：过A作AH⊥BC于H，根据等腰三角形性质得出BH=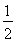BC，∠BAH=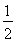∠BAC=60°，求出AE=BE，得出等边三角形ABE，推出AE=AB，根据AAS证△EDA≌△BHA，推出DE=BH即可．

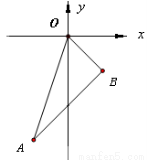
试题解析：如图，过A作AH⊥BC于H，

∵AB=AC，∠BAC=120°，

∴BH=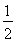BC，∠BAH=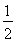∠BAC=60°，∠EAD=60°=∠BAH，

∵DE是线段AB的中垂线，

∴∠EDA=∠AHB=90°，AE=BE，

∴△ABE是等边三角形，

∴AE=AB，

在△EDA和△BHA中

∴△EDA≌△BHA（AAS），

∴DE=BH，

∵BH=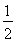BC，

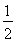∴DE=BC．

考点：1.线段垂直平分线的性质，2.等腰三角形的性质，3.含30度角的直角三角形．