题目内容
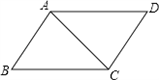
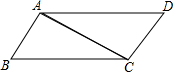 如图,∠DAC=30°,∠B=60°,AB⊥AC,∠D=55°.试判断:
如图,∠DAC=30°,∠B=60°,AB⊥AC,∠D=55°.试判断:
①AD与BC平行吗?
②AB与CD平行吗?为什么?
解:(1)AD∥BC,
理由是:∵AB⊥AC,
∴∠BAC=90°,
∵∠B=60°,
∴∠ACB=180°-90°-60°=30°,
∵∠DAC=30°,
∴∠DAC=∠ACB,
∴AD∥BC;
(2)AB和CD不平行,
理由是:∵∠D=55°,∠DAC=30°,
∴∠DCA=180°-30°-55°=95°,
∵∠BAC=90°,
∴∠DCA≠∠BAC,
∴AB和CD不平行.
分析:(1)求出∠ACB,推出∠ACB=∠DAC,根据平行线的判定推出即可;
(2)求出∠DCA≠∠BAC,根据平行线的判定判断即可.
点评:本题考查了平行线的判定和三角形的内角和定理、垂直定义的应用,注意:平行线的判定定理有:①同位角相等,两直线平行,②内错角相等,两直线平行,③同旁内角互补,两直线平行.
理由是:∵AB⊥AC,
∴∠BAC=90°,
∵∠B=60°,
∴∠ACB=180°-90°-60°=30°,
∵∠DAC=30°,
∴∠DAC=∠ACB,
∴AD∥BC;
(2)AB和CD不平行,
理由是:∵∠D=55°,∠DAC=30°,
∴∠DCA=180°-30°-55°=95°,
∵∠BAC=90°,
∴∠DCA≠∠BAC,
∴AB和CD不平行.
分析:(1)求出∠ACB,推出∠ACB=∠DAC,根据平行线的判定推出即可;
(2)求出∠DCA≠∠BAC,根据平行线的判定判断即可.
点评:本题考查了平行线的判定和三角形的内角和定理、垂直定义的应用,注意:平行线的判定定理有:①同位角相等,两直线平行,②内错角相等,两直线平行,③同旁内角互补,两直线平行.

练习册系列答案
相关题目
 23、如图,∠DAC=30°,∠B=60°,AB⊥AC.
23、如图,∠DAC=30°,∠B=60°,AB⊥AC.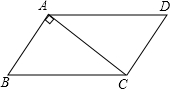 如图,∠DAC=30°,∠B=60°,AB⊥AC.试判断:①AD与BC平行吗?②AB与CD平行吗?为什么?
如图,∠DAC=30°,∠B=60°,AB⊥AC.试判断:①AD与BC平行吗?②AB与CD平行吗?为什么? 如图,∠DAC=30°,∠B=60°,AB⊥AC,∠D=55°.试判断:
如图,∠DAC=30°,∠B=60°,AB⊥AC,∠D=55°.试判断: