题目内容
【题目】如图，AB∥CD，∠CDE=119°，GF交∠DEB的平分线EF于点F，∠AGF=130°，则∠F等于（ ）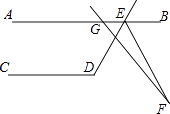 
A.9.5°
B.19°
C.15°
D.30°
【答案】A
【解析】解：∵AB∥CD，∠CDE=119°， ∴∠AED=180°﹣119°=61°，∠DEB=119°．
∵GF交∠DEB的平分线EF于点F，
∴∠DEF= 
×119°=59.5°，
∴∠GEF=61°+59.5°=120.5°．
∵∠AGF=130°，
∴∠F=∠AGF﹣∠GEF=130°﹣120.5°=9.5°．
故选：A．
【考点精析】本题主要考查了角的平分线和平行线的性质的相关知识点，需要掌握从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线；两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补才能正确解答此题．
练习册系列答案
相关题目
