题目内容
如图,B、C为湖中的两个景点.A为游船码头,景点B在景点C的正东,从码头A看景点B在南偏东60°方向,景点C在南偏东30°方向.游船自A以每分钟20米的速度行驶15分钟到达景点C,又以同样的速度驶向景点B,再沿BA驶回码头A.该游船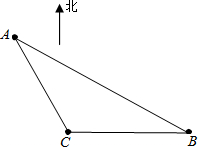 从景点C到景点B需用多长时间?从景点B到码头A需要多长时间?
从景点C到景点B需用多长时间?从景点B到码头A需要多长时间?
( 取1.73,结果保留整数)
取1.73,结果保留整数)
 解:如图,过点A作AD⊥BC,交BC延长线于点D,
解:如图,过点A作AD⊥BC,交BC延长线于点D,得∠DAB=60°,∠DAC=30°,
∴∠DCA=60°,∠BAC=30°.
∴∠B=30°=∠BAC.
∴AC=CB.
∴游船从景点C到景点B需用15分钟.
在Rt△ADC中,AC=300,∠DAC=30°,
∴AD=AC•cos30°=
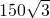 .
.在Rt△ABD中,∠ABD=30°,
∴AB=2AD=
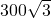 ,
,∴从景点B到码头A的时间为:
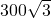 ÷20≈26(分钟).
÷20≈26(分钟).分析:过点A作AD垂直于直线BC,垂足为D,在Rt△ADC中,满足解直角三角形的条件,可以求出AD、DC.在Rt△ADB中,根据解直角三角形的条件求出CB,进而求出时间.
点评:本题考查了解直角三角形的应用,解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
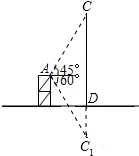 如图,某人在建筑物AB的顶部测得一烟囱CD的顶端C的仰角为45°,测得C在湖中的倒影C1的俯角为60°,已知AB=20m,则烟囱CD的高为
如图,某人在建筑物AB的顶部测得一烟囱CD的顶端C的仰角为45°,测得C在湖中的倒影C1的俯角为60°,已知AB=20m,则烟囱CD的高为 25、万峰湖中学计划用教学楼后宽为20米、长为32米的矩形的空地建造如图所示的农技园,但是要在上面修筑同样宽的两条互相垂直的道路,余下部分作为种植区域,要使种植区域面积为540米2,道路的宽应为多少?
25、万峰湖中学计划用教学楼后宽为20米、长为32米的矩形的空地建造如图所示的农技园,但是要在上面修筑同样宽的两条互相垂直的道路,余下部分作为种植区域,要使种植区域面积为540米2,道路的宽应为多少?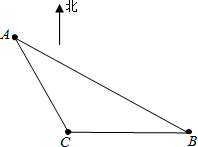 从景点C到景点B需用多长时间?从景点B到码头A需要多长时间?
从景点C到景点B需用多长时间?从景点B到码头A需要多长时间? 取1.73,结果保留整数)
取1.73,结果保留整数)