题目内容
 如图,PT切⊙O于点T,经过圆心O的割线PAB交⊙O于点A、B,已知PT=4,∠P=30°,则⊙O的直径AB等于
如图,PT切⊙O于点T,经过圆心O的割线PAB交⊙O于点A、B,已知PT=4,∠P=30°,则⊙O的直径AB等于分析:连接OT,由切线的性质得到三角形ATO为直角三角形,又∠P=30°,得到OT等于OP的一半,即OA等于OP的一半,进而得到PA,AO,OB都相等,设AP为x,得到PB为3x,由PT的值,利用切割线定理即可列出关于x的方程,求出方程的解即可得到直径AB的长.
解答: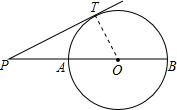 解:连接OT,由PT是⊙O的切线,得到∠PTO=90°,又∠P=30°,
解:连接OT,由PT是⊙O的切线,得到∠PTO=90°,又∠P=30°,
∴OT=
PO,即OA=
OP,
∴PA=OA=OB,设PA=x,则PB=3x,
根据切割线定理得:PT2=PA•PB,即3x2=16,解得x=
,
则AB=2OA=
.
故答案为:
.
 解:连接OT,由PT是⊙O的切线,得到∠PTO=90°,又∠P=30°,
解:连接OT,由PT是⊙O的切线,得到∠PTO=90°,又∠P=30°,∴OT=
| 1 |
| 2 |
| 1 |
| 2 |
∴PA=OA=OB,设PA=x,则PB=3x,
根据切割线定理得:PT2=PA•PB,即3x2=16,解得x=
4
| ||
| 3 |
则AB=2OA=
8
| ||
| 3 |
故答案为:
8
| ||
| 3 |
点评:此题考查学生灵活运用切线性质及切割线定理化简求值,掌握直角三角形中30°角所对的直角边等于斜边的一半,是一道中档题.学生做题时注意已知圆切线时,连接圆心与切点是经常连接的辅助线.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目

 13、已知:如图,PT切⊙O于点T,PA交⊙O于A,B两点且与直径CT交于点D,CD=2,AD=3,BD=6,则PB=
13、已知:如图,PT切⊙O于点T,PA交⊙O于A,B两点且与直径CT交于点D,CD=2,AD=3,BD=6,则PB=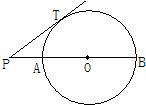 15、如图,PT切⊙O于点T,经过圆心O的割线PAB交⊙O于点A、B,已知PT=4,PA=2,则⊙O的直径AB等于( )
15、如图,PT切⊙O于点T,经过圆心O的割线PAB交⊙O于点A、B,已知PT=4,PA=2,则⊙O的直径AB等于( )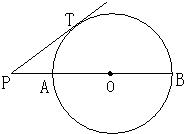 22、如图,PT切⊙O于点T,经过圆心O的割线PAB交⊙O于点A、B,已知PT=4,PA=2,求⊙O的直径AB.
22、如图,PT切⊙O于点T,经过圆心O的割线PAB交⊙O于点A、B,已知PT=4,PA=2,求⊙O的直径AB.