题目内容
为了从甲、乙、丙三名同学中选拔一人参加射击比赛,对他们的射击水平进行了测验,三个人在相同条件下各射击5次,命中的环数如下(单位:环)
甲:6 10 5 10 9
乙:5 9 8 10 8
丙:6 10 4 10 8
(1)求
甲,
乙,
丙,
,
,
;
(2)你认为该选拔哪名同学参加射击比赛?为什么?
甲:6 10 5 10 9
乙:5 9 8 10 8
丙:6 10 4 10 8
(1)求
. |
| x |
. |
| x |
. |
| x |
| s | 2 甲 |
| s | 2 乙 |
| s | 2 丙 |
(2)你认为该选拔哪名同学参加射击比赛?为什么?
分析:(1)根据平均数和方差的定义求解;
(2)首先判断,不会选丙,因为丙的平均成绩差且波动性大,然后比较甲、乙两人的成绩的方差作出判断.
(2)首先判断,不会选丙,因为丙的平均成绩差且波动性大,然后比较甲、乙两人的成绩的方差作出判断.
解答:解:(1)
=
(6+10+5+10+9)=8;
=
(5+9+8+10+8)=8;
=
(6+10+4+10+8)=7.6;
S2甲=
[(6-8)2+(10-8)2+…+(9-8)2]=4.4;
S2乙=
[(5-8)2+(9-8)2+…+(8-8)2]=2.8;
S2丙=
[(6-7.6)2+(10-7.6)2+…+(8-7.6)2]=5.44;
(2)丙的平均成绩差且波动性大,故不能选丙,从方差和平均成绩两个方面来看,应该选乙.
因为甲、乙两名同学射击环数的平均数相同,乙同学射击的方差小于甲同学的方差,乙同学的成绩较稳定,应选乙参加比赛.
. |
| x甲 |
| 1 |
| 5 |
. |
| x乙 |
| 1 |
| 5 |
. |
| x丙 |
| 1 |
| 5 |
S2甲=
| 1 |
| 5 |
S2乙=
| 1 |
| 5 |
S2丙=
| 1 |
| 5 |
(2)丙的平均成绩差且波动性大,故不能选丙,从方差和平均成绩两个方面来看,应该选乙.
因为甲、乙两名同学射击环数的平均数相同,乙同学射击的方差小于甲同学的方差,乙同学的成绩较稳定,应选乙参加比赛.
点评:本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为
,则方差S2=
[(x1-x?)2+(x2-x?)2+…+(xn-x?)2](可简单它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
. |
| x |
| 1 |
| n |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
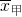 ,
,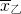 ,
,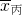 ,
,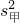 ,
,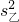 ,
,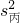 ;
; ,
, ,
, ;
; ,
, ,
, ;
;