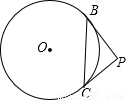
题目内容
 如图所示,圆上有B,C两点,PB,PC为圆的两切线.若
如图所示,圆上有B,C两点,PB,PC为圆的两切线.若 将圆分成两弧,且其中一弧的长为圆周长的
将圆分成两弧,且其中一弧的长为圆周长的 ,则∠BPC的度数为
,则∠BPC的度数为
- A.108
- B.120
- C.144
- D.162
C
分析:设圆的圆心为O,连接OB、OC,由于弧BC是圆的 ,即圆心角∠BOC=36°;而PB、PC同为⊙O的切线,那么∠OBP、∠OCP都为直角,则∠BOC、∠BPC互补,由此得解.
,即圆心角∠BOC=36°;而PB、PC同为⊙O的切线,那么∠OBP、∠OCP都为直角,则∠BOC、∠BPC互补,由此得解.
解答: 解:设圆心为O,连接OB、OC;
解:设圆心为O,连接OB、OC;
则∠OBP=∠OCP=90°;
∵劣弧BC是圆周长的 ,
,
∴∠BOC=360°× =36°;
=36°;
∴∠BPC=180°-∠BOC=144°.
故选C.
点评:此题主要考查了切线的性质以及四边形的内角和,能够正确作出辅助线是解题的关键.
分析:设圆的圆心为O,连接OB、OC,由于弧BC是圆的
 ,即圆心角∠BOC=36°;而PB、PC同为⊙O的切线,那么∠OBP、∠OCP都为直角,则∠BOC、∠BPC互补,由此得解.
,即圆心角∠BOC=36°;而PB、PC同为⊙O的切线,那么∠OBP、∠OCP都为直角,则∠BOC、∠BPC互补,由此得解.解答:
 解:设圆心为O,连接OB、OC;
解:设圆心为O,连接OB、OC;则∠OBP=∠OCP=90°;
∵劣弧BC是圆周长的
 ,
,∴∠BOC=360°×
 =36°;
=36°;∴∠BPC=180°-∠BOC=144°.
故选C.
点评:此题主要考查了切线的性质以及四边形的内角和,能够正确作出辅助线是解题的关键.

练习册系列答案
相关题目
 如图所示,圆上有B,C两点,PB,PC为圆的两切线.若
如图所示,圆上有B,C两点,PB,PC为圆的两切线.若 |
| BC |
| 1 |
| 10 |
| A、108 | B、120 |
| C、144 | D、162 |
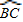 将圆分成两弧,且其中一弧的长为圆周长的
将圆分成两弧,且其中一弧的长为圆周长的 ,则∠BPC的度数为( )
,则∠BPC的度数为( )
 将圆分成两弧,且其中一弧的长为圆周长的
将圆分成两弧,且其中一弧的长为圆周长的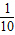 ,则∠BPC的度数为( )
,则∠BPC的度数为( )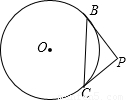
 将圆分成两弧,且其中一弧的长为圆周长的
将圆分成两弧,且其中一弧的长为圆周长的 ,则∠BPC的度数为( )
,则∠BPC的度数为( )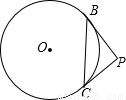
 将圆分成两弧,且其中一弧的长为圆周长的
将圆分成两弧,且其中一弧的长为圆周长的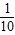 ,则∠BPC的度数为( )
,则∠BPC的度数为( )