题目内容
AB是⊙O的直径,点E是半圆上一动点(点E与点A、B都不重合),点C是BE延长线上的一点,且CD⊥AB,垂足为D,CD与AE交于点H,点H与点A不重合。

(1)(5分)求证:△AHD∽△CBD
(2)(4分)连HB,若CD=AB=2,求HD+HO的值
(1)证明略
(2)1
解析:(1)证明:略
(2)设OD=x,则BD=1-x,AD=1+x
证Rt△AHD∽Rt△CBD
则HD : BD=AD : CD
即HD : (1-x)=(1+x) : 2
即HD=
在Rt△HOD中,由勾股定理得:
OH==
所以HD+HO=+
=1
注意:当点E移动到使D与O重合的位置时,这时HD与HO重合,
由Rt△AHO∽Rt△CBO,利用对应边的比例式为方程,可以算出HD=HO=,即HD+HO=1

练习册系列答案
相关题目
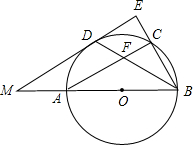 如图,AB是⊙O的直径,点D是
如图,AB是⊙O的直径,点D是
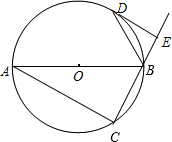 已知:如图,AB是⊙O的直径,点C在⊙O上,△ABC的外角平分线BD交⊙O于D,DE与⊙O相切,交CB的延长线于E.
已知:如图,AB是⊙O的直径,点C在⊙O上,△ABC的外角平分线BD交⊙O于D,DE与⊙O相切,交CB的延长线于E. (2013•淮北模拟)如图,已知AB是⊙O的直径,点C、D在⊙O上,且AB=10,AC=8.
(2013•淮北模拟)如图,已知AB是⊙O的直径,点C、D在⊙O上,且AB=10,AC=8.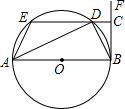 如图,AB是⊙O的直径,点C在⊙O的切线BF上,过C作直线CE⊥BF,交⊙O于点D、点E,连接AE、
如图,AB是⊙O的直径,点C在⊙O的切线BF上,过C作直线CE⊥BF,交⊙O于点D、点E,连接AE、