Question

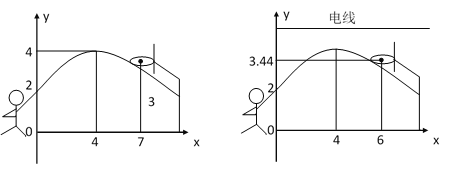
【题目】在小明的一次投篮中，球出手时离地面高2米，与篮圈中心的水平距离为7米，当球出手后水平距离为4米时到达最大高度4米．篮球运行的轨迹为抛物线，篮球中心距离地面3米，通过计算说明此球能否投中．

探究一：若出手的角度、力度和高度都不变的情况下，求小明朝着篮球架再向前平移多少米后跳起投篮也能将篮球投入篮筐中？

探究二：若出手的角度、力度和高度都发生改变的情况下，但是抛物线的顶点等其他条件不变，求小明出手的高度需要增加多少米才能将篮球投入篮筐中？

探究三：若出手的角度、力度都改变，出手高度不变，篮筐的坐标为（6，3.44），球场上方有一组高6米的电线，要想在篮球不触碰电线的情况下，将篮球投入篮筐中，直接写出二次函数解析式中a的取值范围．

Answer 1

【答案】探究一：3-米；探究二：米；探究三：-＜a≤-．

【解析】

根据题意列出解析式，再将数据代入求值判断即可，根据每个探究的题意列式计算即可．

解：因为抛物线的顶点为（4，4），设抛物线的解析式为y=a（x-4）2+4，

∵过点（0，2），

∴2=16a+4，

∴a=-，即y=-（x-4）2+4，

当x=7时，y=-+4=≠3．所以此球不能投中．

探究一：设向前平移h米，由题意可得y=-（x-4-h）2+4，代入点（7，3），

得3=-（7-4-h）2+4求得h=3±，

根据实际情况h=3-，即向前平移3-米，可投中篮筐；

探究二：设y=a（x-4）2+4，

因为投中篮筐，即代入x=7，y=3得3=a（7-4）2+4，

解得a=-，即y=-（x-4）2+4，

当x=0时，y=，-2=即小明出手的高度要增加米，可将篮球投中；

探究三：设y=a（x-b）2+6，代入点（0，2）（6，3.44）得，

解得a=-，设y=a（x-6）2+3.44，

∵过点（0，2）代入得2=36a+3.44，

得a=-，所以-＜a≤-．