题目内容
(2000•山西)请阅读下面材料,并回答所提出的问题.三角形内角平分线性质定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.
已知:如图,△ABC中,AD是角平分线.
求证:
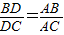
分析:要证
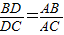 ,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式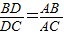 中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明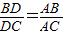 就可以转化成证AE=AC.
就可以转化成证AE=AC.证明:过C作CE∥DA,交BA的延长线于E.
CE∥DA
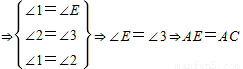 ,
,CE∥DA
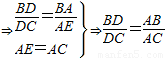
(1)上述证明过程中,用到了哪些定理?(写对两个定理即可)
(2)在上述分析、证明过程中,主要用到了下列三种数学思想的哪一种?选出一个填在后面的括号内.[]
①数形结合思想;
②转化思想;
③分类讨论思想.
(3)用三角形内角平分线性质定理解答问题:
已知:如图,△ABC中,AD是角平分线,AB=5cm,AC=4cm,BC=7cm.求BD的长.

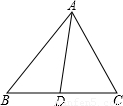
【答案】分析:(1)由比例式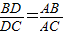 ,想到作平行线,用到了平行线的性质定理;只要证明AE=AC即可,用到了等腰三角形的判定定理;由CE∥AD,写出比例式
,想到作平行线,用到了平行线的性质定理;只要证明AE=AC即可,用到了等腰三角形的判定定理;由CE∥AD,写出比例式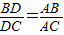 ,用到了平行线分线段成比例定理(推论);
,用到了平行线分线段成比例定理(推论);
(2)把AC转化成AE,是用的转化思想;
(3)利用三角形内角平分线性质定理,列出比例式,代入数据计算出结果.
解答:解:(1)证明过程中用到的定理有:
①平行线的性质定理;
②等腰三角形的判定定理;
(2)②转化思想.(4分)
(3)∵AD是角平分线,
∴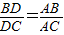 (5分)
(5分)
又∵AB=5,AC=4,BC=7,
∴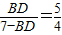 ,
,
∴BD=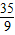 (cm).
(cm).
点评:此题是一道材料题,根据材料推得的结果进行解题,主要考查平行线分线段成比例定理的理解及运用.
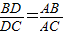 ,想到作平行线,用到了平行线的性质定理;只要证明AE=AC即可,用到了等腰三角形的判定定理;由CE∥AD,写出比例式
,想到作平行线,用到了平行线的性质定理;只要证明AE=AC即可,用到了等腰三角形的判定定理;由CE∥AD,写出比例式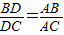 ,用到了平行线分线段成比例定理(推论);
,用到了平行线分线段成比例定理(推论);(2)把AC转化成AE,是用的转化思想;
(3)利用三角形内角平分线性质定理,列出比例式,代入数据计算出结果.
解答:解:(1)证明过程中用到的定理有:
①平行线的性质定理;
②等腰三角形的判定定理;
(2)②转化思想.(4分)
(3)∵AD是角平分线,
∴
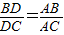 (5分)
(5分)又∵AB=5,AC=4,BC=7,
∴
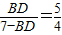 ,
,∴BD=
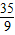 (cm).
(cm).点评:此题是一道材料题,根据材料推得的结果进行解题,主要考查平行线分线段成比例定理的理解及运用.

练习册系列答案
相关题目


 ,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式 中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明 就可以转化成证AE=AC.
就可以转化成证AE=AC. ,
,



 ,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式 中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明 就可以转化成证AE=AC.
就可以转化成证AE=AC. ,
,



 ,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式
,一般只要证BD、DC与AB、AC或BD、AB与DC、AC所在三角形相似.现在B、D、C在一直线上,△ABD与△ADC不相似,需要考虑用别的方法换比.在比例式 中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明
中,AC恰是BD、DC、AB的第四比例项,所以考虑过C作CE∥AD,交BA的延长线于E,从而得到BD、DC、AB的第四比例项AE,这样,证明 就可以转化成证AE=AC.
就可以转化成证AE=AC. ,
,

