题目内容
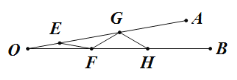
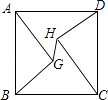
【题目】如图,将Rt△ABC绕直角顶点A顺时针旋转90°,得到△AB′C′,连结BB′,若∠1=20°,则∠C的度数是 . 
【答案】65°
【解析】解:∵△ABC是直角三角形,
∴∠BAC=90°,
∵Rt△ABC绕直角顶点A顺时针旋转90°,
∴AB=AB′,∠BAB′=90°,∠C=∠AC′B′,
∴∠AB′B=45°,
∵∠1=20°,
∴∠AB′C′=45°﹣20°=25°,
∴∠AC′B′=90°﹣25°=65°,
∴∠C=65°,
所以答案是:65°.
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角,以及对等腰三角形的性质的理解,了解等腰三角形的两个底角相等(简称:等边对等角).

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目