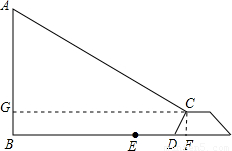
题目内容
 我市城市规划期间,欲拆除沿江路一电线杆AB(如图),已知望月堤D距电线杆AB水平距离为14m,背水面CD的坡度i=2:1,堤高CF为2m,在堤顶C处测得杆顶A的仰角为30°,D、E之间是宽为2m的人行道,试问在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上,请说明理由.(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域)(
我市城市规划期间,欲拆除沿江路一电线杆AB(如图),已知望月堤D距电线杆AB水平距离为14m,背水面CD的坡度i=2:1,堤高CF为2m,在堤顶C处测得杆顶A的仰角为30°,D、E之间是宽为2m的人行道,试问在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上,请说明理由.(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域)(| 3 |
| 2 |
分析:根据题意分析图形可得:在Rt△CDF中,由CF=2,tan∠CDF=2,可求得DE,进而得到BE的长.解Rt△AGC可得BE的值,通过比较BE、AB的大小即可求出答案.
解答:解:由tan∠CDF=
=2,CF=2米,
∴DF=1米,BG=2米;
∵BD=14米,
∴BF=GC=15米;
在Rt△AGC中,由tan30°=
,
∴AG=15×
≈5×1.732=8.660米;
∴AB=8.660+2=10.66米;
而BE=BD-ED=12米,
∴BE>AB;
因此不需要封人行道.
| CF |
| DF |

∴DF=1米,BG=2米;
∵BD=14米,
∴BF=GC=15米;
在Rt△AGC中,由tan30°=
| ||
| 3 |
∴AG=15×
| ||
| 3 |
∴AB=8.660+2=10.66米;
而BE=BD-ED=12米,
∴BE>AB;
因此不需要封人行道.
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
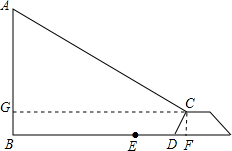 我市城市规划期间,欲拆除沿江路一电线杆AB(如图),已知望月堤D距电线杆AB水平距离为14m,背水面CD的坡度i=2:1,堤高CF为2m,在堤顶C处测得杆顶A的仰角为30°,D、E之间是宽为2m的人行道,试问在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上,请说明理由.(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域)(
我市城市规划期间,欲拆除沿江路一电线杆AB(如图),已知望月堤D距电线杆AB水平距离为14m,背水面CD的坡度i=2:1,堤高CF为2m,在堤顶C处测得杆顶A的仰角为30°,D、E之间是宽为2m的人行道,试问在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上,请说明理由.(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域)( ,
, )
)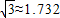 ,
,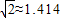 )
)