题目内容
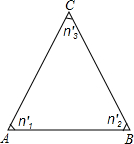（2013•曲靖）如图，将△ABC绕其中一个顶点顺时针连续旋转n′1、n′2、n′3所得到的三角形和△ABC的对称关系是关于旋转点成中心对称
关于旋转点成中心对称
．分析：先根据三角形内角和为180°得出n′1+n′2+n′3=180°，再由旋转的定义可知，将△ABC绕其中一个顶点顺时针旋转180°所得到的三角形和△ABC关于这个点成中心对称．
解答：解：∵n′1+n′2+n′3=180°，
∴将△ABC绕其中一个顶点顺时针连续旋转n′1、n′2、n′3，就是将△ABC绕其中一个顶点顺时针旋转180°，
∴所得到的三角形和△ABC关于这个点成中心对称．
故答案为：关于旋转点成中心对称．
∴将△ABC绕其中一个顶点顺时针连续旋转n′1、n′2、n′3，就是将△ABC绕其中一个顶点顺时针旋转180°，
∴所得到的三角形和△ABC关于这个点成中心对称．
故答案为：关于旋转点成中心对称．
点评：本题考查了三角形内角和定理，旋转的定义与性质，比较简单．正确理解顺时针连续旋转n′1、n′2、n′3，就是顺时针旋转180°是解题的关键．
练习册系列答案
相关题目
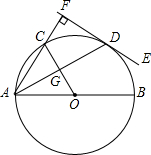（2013•曲靖）如图，⊙O的直径AB=10，C、D是圆上的两点，且
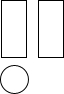（2013•曲靖）如图是某几何体的三视图，则该几何体的侧面展开图是（ ）
（2013•曲靖）如图，在?ABCD中，对角线AC与BD相交于点O，过点O作EF⊥AC交BC于点E，交AD于点F，连接AE、CF．则四边形AECF是（ ）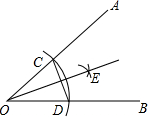
（2013•曲靖）如图，以∠AOB的顶点O为圆心，适当长为半径画弧，交OA于点C，交OB于点D．再分别以点C、D为圆心，大于
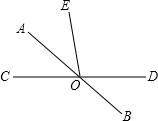（2013•曲靖）如图，直线AB、CD相交于点O，若∠BOD=40°，OA平分∠COE，则∠AOE=