题目内容
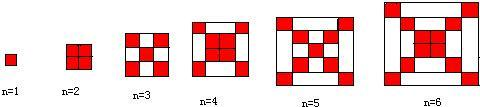
如图每个正方形是由边长为1的小正方形组成.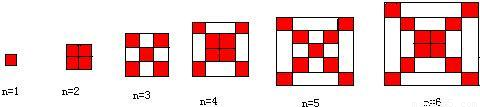
(1)观察图形,请填与下列表格:
| 正方形边长 | 1 | 3 | 5 | 7 | … | n(奇数) |
| 红色小正方形个数 | … |
| 正方形边长 | 2 | 4 | 6 | 8 | … | n(偶数) |
| 红色小正方形个数 | … |
【答案】分析:(1)此题找规律时,显然应分两种情况分析:当n是奇数时,红色小正方形的个数是对应的奇数;当n是偶数时,红色小正方形的个数是对应的偶数.
(2)分别表示偶数时P1和P2的值,然后列方程求解,进行分析.
解答:解:(1)1,5,9,13,…,则(奇数)2n-1;4,8,12,16,…,则(偶数)2n.
(2)由(1)可知n为偶数时P1=2n,白色与红色的总数为n2,
∴P2=n2-2n,
根据题意假设存在,则n2-2n=5×2n,
n2-12n=0,
解得n=12,n=0(不合题意舍去).
存在偶数n=12使得P2=5P1.
点评:此题的难点在于必须分情况找规律.
(2)分别表示偶数时P1和P2的值,然后列方程求解,进行分析.
解答:解:(1)1,5,9,13,…,则(奇数)2n-1;4,8,12,16,…,则(偶数)2n.
(2)由(1)可知n为偶数时P1=2n,白色与红色的总数为n2,
∴P2=n2-2n,
根据题意假设存在,则n2-2n=5×2n,
n2-12n=0,
解得n=12,n=0(不合题意舍去).
存在偶数n=12使得P2=5P1.
点评:此题的难点在于必须分情况找规律.

练习册系列答案
相关题目
如图每个正方形是由边长为1的小正方形组成.
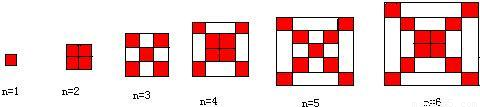
(1)观察图形,请填与下列表格:
(2)在边长为n(n≥1)的正方形中,设红色小正方形的个数为P1,白色小正方形的个数为P2,问是否存在偶数n,使P2=5P1?若存在,请写出n的值;若不存在,请说明理由.

(1)观察图形,请填与下列表格:
| 正方形边长 | 1 | 3 | 5 | 7 | … | n(奇数) |
| 红色小正方形个数 | … |
| 正方形边长 | 2 | 4 | 6 | 8 | … | n(偶数) |
| 红色小正方形个数 | … |
如图每个正方形是由边长为1的小正方形组成.

(1)观察图形,请填与下列表格:
(2)在边长为n(n≥1)的正方形中,设红色小正方形的个数为P1,白色小正方形的个数为P2,问是否存在偶数n,使P2=5P1?若存在,请写出n的值;若不存在,请说明理由.

(1)观察图形,请填与下列表格:
| 正方形边长 | 1 | 3 | 5 | 7 | … | n(奇数) |
| 红色小正方形个数 | … |
| 正方形边长 | 2 | 4 | 6 | 8 | … | n(偶数) |
| 红色小正方形个数 | … |
如图每个正方形是由边长为1的小正方形组成.

(1)观察图形,请填与下列表格:
(2)在边长为n(n≥1)的正方形中,设红色小正方形的个数为P1,白色小正方形的个数为P2,问是否存在偶数n,使P2=5P1?若存在,请写出n的值;若不存在,请说明理由.

(1)观察图形,请填与下列表格:
| 正方形边长 | 1 | 3 | 5 | 7 | … | n(奇数) |
| 红色小正方形个数 | … |
| 正方形边长 | 2 | 4 | 6 | 8 | … | n(偶数) |
| 红色小正方形个数 | … |