题目内容
【题目】如图,在⊙O中,直径AB平分弦CD,AB与CD相交于点E,连接AC、BC,点F是BA延长线上的一点,且∠FCA=∠B.
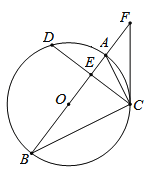
(1)求证:CF是⊙O的切线.
(2)若AC=4,tan∠ACD![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)利用圆周角定理以及等腰三角形的性质得出∠OCF=90°,进而得出答案;
(2)利用垂径定理推论得出![]() ,进而得出BC的长,再利用勾股定理求出即可.
,进而得出BC的长,再利用勾股定理求出即可.
试题解析:(1)连接CO,
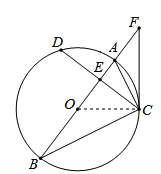
∵AB是⊙O的直径,
∴∠BCA=90°,
∴∠ACO+∠OCB=90°,
∵OB=CO,
∴∠B=∠OCB,
∵∠FCA=∠B,
∴∠BCO=∠ACF,
∴∠OCA+∠ACF=90°,
即∠OCF=90°,
∴CF是⊙O的切线;
(2)∵直径AB平分弦CD,
∴AB⊥DC,
∴![]() ,
,
∵AC=4,tan∠ACD=![]() ,
,
∴tan∠B=tan∠ACD=![]() ,
,
∴![]()
∴BC=8,
∴在Rt△ABC中,
AB=![]()
则⊙O的半径为:![]() .
.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目