题目内容
 观察如图所示的图形,回答下列问题:
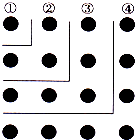
观察如图所示的图形,回答下列问题:(1)图中的点被线段隔开分成四层,则第一层有1个点,第二层有3个点,第三层有5个点,第四层有
7
7
个点;(2)如果要你继续画下去,那么第五层有多少个点?第n层呢?
(3)某一层上有77个点,你知道这是第几层吗?
(4)第一层与第二层的和是多少?前三层的和是多少?前四层呢?你有没有发现什么规律(用含n的代数式表示)?根据你的推测,前十二层的和是多少?
分析:(1)根据图形中点的个数直接得出答案即可;
(2)根据每层的点的个数变化规律得出答案即可;
(3)根据(2)中所求的规律得出一元一次方程解出即可;
(4)根据图形直接得出前几层的点的个数变化规律,进而得出答案.
(2)根据每层的点的个数变化规律得出答案即可;
(3)根据(2)中所求的规律得出一元一次方程解出即可;
(4)根据图形直接得出前几层的点的个数变化规律,进而得出答案.
解答:解;(1)如图所示:第四层有7个点;
故答案为:7;
(2)∵第一层有1个点,第二层有3个点,第三层有5个点,第四层有7个点,
∴如果继续画下去,那么第五层有9个点,第n层有(2n-1)个点;
(3)某一层上有77个点,即:2n-1=77,
解得:n=39,
∴这是第三十九层;
(4)∵第一层与第二层的和是4,前三层的和是9,前四层的和是16,…,前n层的和是n 2,
∴前十二层的和是144.
故答案为:7;
(2)∵第一层有1个点,第二层有3个点,第三层有5个点,第四层有7个点,
∴如果继续画下去,那么第五层有9个点,第n层有(2n-1)个点;
(3)某一层上有77个点,即:2n-1=77,
解得:n=39,
∴这是第三十九层;
(4)∵第一层与第二层的和是4,前三层的和是9,前四层的和是16,…,前n层的和是n 2,
∴前十二层的和是144.
点评:此题主要考查了数字变化规律,根据已知得出数据中的变与不变是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 20、观察如图所示的图形是否有其中一个图形,是另一个图形经旋转得到的.
20、观察如图所示的图形是否有其中一个图形,是另一个图形经旋转得到的.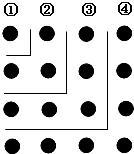 010,即第2004层有2 009 010个正方体.
010,即第2004层有2 009 010个正方体.