题目内容
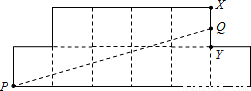
 图中的八边形是由10个单位正方形所组成的,在PQ下面的部分包含一个单位正方形与底边为5的三角形.若PQ恰将这八边形平分成两个面积相等的部分,则
图中的八边形是由10个单位正方形所组成的,在PQ下面的部分包含一个单位正方形与底边为5的三角形.若PQ恰将这八边形平分成两个面积相等的部分,则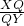 之值为________?
之值为________?
(A)  (B)
(B)  (C)
(C)  (D)
(D)  (E)
(E)  .
.
D
分析:首先设QY=x,则XQ=1-x,根据题意得到:PQ下面的部分的面积为:S△+S正方形= ×5×(1+x)+1=5,解方程即可求得结果.
×5×(1+x)+1=5,解方程即可求得结果.
解答:设QY=x,则XQ=1-x,
∵PQ恰将这八边形平分成两个面积相等的部分,
∴PQ下面的部分的面积为:S△+S正方形= ×5×(1+x)+1=5,
×5×(1+x)+1=5,
解得:x= ,
,
∴QY= ,
,
则XQ=1-x=1- =
= ,
,
∴XQ:QY= :
: =2:3.
=2:3.
故选D.
点评:此题考查了不规则图形的面积的求解方法:注意将原图形分割求解.此题难度不大,要注意仔细识图.
分析:首先设QY=x,则XQ=1-x,根据题意得到:PQ下面的部分的面积为:S△+S正方形=
 ×5×(1+x)+1=5,解方程即可求得结果.
×5×(1+x)+1=5,解方程即可求得结果.解答:设QY=x,则XQ=1-x,
∵PQ恰将这八边形平分成两个面积相等的部分,
∴PQ下面的部分的面积为:S△+S正方形=
 ×5×(1+x)+1=5,
×5×(1+x)+1=5,解得:x=
 ,
,∴QY=
 ,
,则XQ=1-x=1-
 =
= ,
,∴XQ:QY=
 :
: =2:3.
=2:3.故选D.
点评:此题考查了不规则图形的面积的求解方法:注意将原图形分割求解.此题难度不大,要注意仔细识图.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
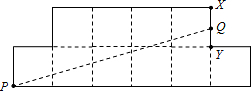 图中的八边形是由10个单位正方形所组成的,在PQ下面的部分包含一个单位正方形与底边为5的三角形.若PQ恰将这八边形平分成两个面积相等的部分,则
图中的八边形是由10个单位正方形所组成的,在PQ下面的部分包含一个单位正方形与底边为5的三角形.若PQ恰将这八边形平分成两个面积相等的部分,则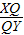 之值为 ?
之值为 ? (B)
(B)  (C)
(C)  (D)
(D)  (E)
(E)  .
.