题目内容
【题目】已知⊙O的直径20,OP长为8,则过P的弦中,弦长为整数的弦共有( )条.
A.1 B.9 C.17 D.16
【答案】D
【解析】
试题分析:求出过P点的弦的长度的取值范围,取特殊解,根据对称性综合求解.
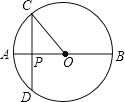
解:如图,AB是直径,OA=10,OP=8,过点P作CD⊥AB,交圆于点C,D两点.
由垂径定理知,点P是CD的中点,
∴PC=4,
在直角三角形OPC中,由勾股定理求得,PC=6,
∴CD=12,则CD是过点P最短的弦长为12;AB是过P最长的弦,长为20.
故过点P的弦的长度都在12~20之间;
因此弦长为12,13,14,15,16,17,18,19,20;
当弦长为12、20时,过P点的弦分别为弦CD和过P点的直径,分别有一条;
当弦长为13,14,15,16,17,18,19时,根据圆的对称性知,符合条件的弦应该有两条;
故弦长为整数的弦共有16条.
故选D.

练习册系列答案
相关题目