题目内容
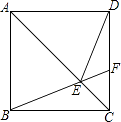
【题目】如图,已知正方形ABCD的边长为12,BM=CN=5,CM,DN交于点O.则下列结论: 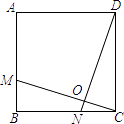
①DN⊥MC;②DN垂直平分MC;③sin∠OCD= ![]() ;④S△ODC=S四边形BMON中,
;④S△ODC=S四边形BMON中,
正确的有(填写序号)
【答案】①③④
【解析】解:∵四边形ABCD是正方形, ∴BC=CD,∠ABC=∠BCD=90°,
在△BMC和△CND中, ,
,
∴△BMC≌△CND,
∴∠MCB=∠NDC.
又∠MCN+∠MCD=90°,
∴∠MCD+∠NDC=90°,
∴∠DOC=90°,
∴DN⊥MC,故①正确;
在Rt△CDN中,∵CD=12,CN=5,
∴DN= ![]() =13.
=13.
又∵∠BCD=90°,∠COD=90°
∴ ![]() NCCD=
NCCD= ![]() NDOC,
NDOC,
∴OC= ![]() ,OM=13﹣
,OM=13﹣ ![]() =
= ![]() ,
,
∴OC≠OM,故②错误;
∵∠DNC+∠NDC=90°,∠ODC+∠OCD=90°,
∴∠OCD=∠DNC,
∴sin∠OCD=sin∠DNC= ![]() =
= ![]() ,故③正确;
,故③正确;
∵△BMC≌△CND,
∴S△BMC=S△CND
S△BMC﹣S△CNC=S△CND﹣S△CNC , 即S四边形BMON=S△ODC , 故④正确.
综上,正确的结论是①③④.
所以答案是①③④.
【考点精析】本题主要考查了勾股定理的概念和正方形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目