题目内容
如图，∠ABC=90°，O为射线BC上一点，以点O为圆心，
OB长为半径作⊙O，将射线BA绕点B按顺时针方向旋转至BA′，若BA′与⊙O相切，则旋转的角度α（0°＜α＜180°）等于________．
60°或120°
分析：当BA′与⊙O相切时，可连接圆心与切点，通过构建的直角三角形，求出∠A′BO的度数，然后再根据BA′的不同位置分类讨论．
解答：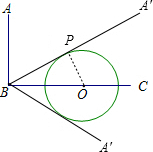
解：如图；
①当BA′与⊙O相切，且BA′位于BC上方时，设切点为P，连接OP，则∠OPB=90°；
Rt△OPB中，OB=2OP，
∴∠A′BO=30°；
∴∠ABA′=60°；
②当BA′与⊙O相切，且BA′位于BC下方时；
同①，可求得∠A′BO=30°；
此时∠ABA′=90°+30°=120°；
故旋转角α的度数为60°或120°．
点评：此题主要考查的是切线的性质，以及解直角三角形的应用；需注意切线的位置有两种情况，不要漏解．
分析：当BA′与⊙O相切时，可连接圆心与切点，通过构建的直角三角形，求出∠A′BO的度数，然后再根据BA′的不同位置分类讨论．
解答：
解：如图；①当BA′与⊙O相切，且BA′位于BC上方时，设切点为P，连接OP，则∠OPB=90°；
Rt△OPB中，OB=2OP，
∴∠A′BO=30°；
∴∠ABA′=60°；
②当BA′与⊙O相切，且BA′位于BC下方时；
同①，可求得∠A′BO=30°；
此时∠ABA′=90°+30°=120°；
故旋转角α的度数为60°或120°．
点评：此题主要考查的是切线的性质，以及解直角三角形的应用；需注意切线的位置有两种情况，不要漏解．
练习册系列答案
阅读快车系列答案
相关题目
3、如图，∠ABC=90°，BD⊥AC，垂足为D，则能表示点到直线（或线段）的距离的线段有（ ）
如图，∠ABC=90°，BC=4，AC=5，以BC为公共边的直角△BCD与△ABC相似，且D、A在BC的两侧，求BD的长．（只要写出两种情况即可）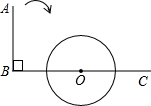
如图，∠ABC=90°，O为射线BC上一点，以点O为圆心、
（2012•大兴区二模）已知：如图，∠ABC=90°，DC⊥BC，E，F为BC上两点，且BE=CF，AB=DC．
如图，∠ABC=90°，AB=4cm，BC=2cm，C到AB的距离为