题目内容
完成下列各题(1)已知函数y=2x2-ax-a2,当x=1时,y=0,求a的值.
(2)若分式
| x2-3x-4 |
| |x-3|-1 |
(3)关于x的方程(1-2k)x2-2(k+1)x-
| 1 |
| 2 |
①若方程只有一个实根,求出这个根;
②若方程有两个不相等的实根x1,x2,且
| 1 |
| x1 |
| 1 |
| x2 |
分析:(1)把x=1,y=0的值代入原函数,得出关于a的方程求出a的值.
(2)分式的值是0,则分子等于0,且分母不等于0,据此即可求得;
(3)①若方程只有一个实根,则方程是一元一次方程,根据定义即可求得k的值;
②
+
=-6即
=-6,根据一元二次方程中根与系数的关系,表示出两根的和与两根的积,代入即可得到关于k的方程,从而求解.
(2)分式的值是0,则分子等于0,且分母不等于0,据此即可求得;
(3)①若方程只有一个实根,则方程是一元一次方程,根据定义即可求得k的值;
②
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
解答:解:(1)∵x=1时,y=0,
?0=2×12-a×1-a2,
解得:a1=-2,a2=1;
(2)由题意得:x2-3x-4=0且|x-3|-1≠0得,
(x-4)(x+1)=0,
解得x1=4,x2=-1;
验证当x=4时,|x-3|-1=0,
当x=-1时,|x-3|-1≠0
∴x=-1.
(3)①方程只有一个实数根,故方程是一元一次方程.
∴1-2k=0即k=
,
则此时方程为:-2×
x-
×
=0,
解得:x=-
;
②由根与系数的关系得:
∵x1+x2=
,x1x2=-
,
又∵
+
=-6
∴
=-6,
∴
=
,
∵1-2k≠0,
∴2(k+1)=3k,
∴k=2.
经检验k=2是方程的根.
?0=2×12-a×1-a2,
解得:a1=-2,a2=1;
(2)由题意得:x2-3x-4=0且|x-3|-1≠0得,
(x-4)(x+1)=0,
解得x1=4,x2=-1;
验证当x=4时,|x-3|-1=0,
当x=-1时,|x-3|-1≠0
∴x=-1.
(3)①方程只有一个实数根,故方程是一元一次方程.
∴1-2k=0即k=
| 1 |
| 2 |
则此时方程为:-2×
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:x=-
| 1 |
| 12 |
②由根与系数的关系得:
∵x1+x2=
| 2(k+1) |
| 1-2k |
| k |
| 2(1-2k) |
又∵
| 1 |
| x1 |
| 1 |
| x2 |
∴
| x1+x2 |
| x1x2 |
∴
| 2(k+1) |
| 1-2k |
| 6k |
| 2(1-2k) |
∵1-2k≠0,
∴2(k+1)=3k,
∴k=2.
经检验k=2是方程的根.
点评:本题考查了一元二次方程的解法,解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法,此题主要考根的判别式及根与系数的关系的综合运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
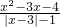 的值为零,求x的值.
的值为零,求x的值. 有实根.
有实根. ,求k的值.
,求k的值.