题目内容
17.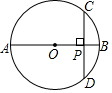 ⊙O的直径AB=10cm,弦CD⊥AB,垂足为P.若OP:OB=3:5,则CD的长为( )
⊙O的直径AB=10cm,弦CD⊥AB,垂足为P.若OP:OB=3:5,则CD的长为( )| A. | 6cm | B. | 4cm | C. | 8cm | D. | $\sqrt{91}$cm |
分析 连结OC,先计算出OP=3cm,再由CD⊥AB,根据垂径定理得到CP=DP,然后根据勾股定理可计算出PC=4cm,于是得到CD=8cm.
解答 解:连接OC,
∵AB=10cm,
∴OB=5cm;
∵OP:OB=3:5,
∴OP=3cm;
Rt△OCP中,OC=OB=5cm,OP=3cm;
由勾股定理,得:CP=$\sqrt{O{C}^{2}-O{P}^{2}}$=4cm;
∴CD=2PC=8cm,
故选C.
点评 本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列数据:20,22,25,24,25的众数和中位数分别为( )
| A. | 20和24 | B. | 25和20 | C. | 25和24 | D. | 25和22 |
5.下列计算正确的是( )
| A. | sin60°-sin30°=sin30° | B. | sin245°+cos245°=1 | ||
| C. | cos60$°=\frac{sin60°}{cos60°}$ | D. | cos30$°=\frac{cos30°}{sin30°}$ |
12.对于反比例函数y=-$\frac{3}{x}$,下列说法错误的是( )
| A. | 经过点(3,-1) | |
| B. | 在第二象限内,y随x的增大而增大 | |
| C. | 是轴对称图形,且对称轴是y轴 | |
| D. | 是中心对称图形,且对称中心是坐标原点 |
 如图,OP平分∠AOB,PD⊥OB于D,∠OPD=60°,PO=4,则点P到边OA的距离是2.
如图,OP平分∠AOB,PD⊥OB于D,∠OPD=60°,PO=4,则点P到边OA的距离是2.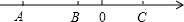 如图,数轴上的三个点A、B、C分别表示有理数a、b、c,化简2|a-b|-|b+c|+|c-a|-|b-c|.
如图,数轴上的三个点A、B、C分别表示有理数a、b、c,化简2|a-b|-|b+c|+|c-a|-|b-c|.