��Ŀ����
��ѧѧϰ��������ѧ֪ʶ������������ʷһ����������Դ�ڲ²��еķ��֣����������ֵIJ�һ���ԣ����ǵ������������е�֪ʶ��Ϊ������ǰ����֤֮�������ֵ�������û��ì��֮�Ϳ�����Ϊ�µ�������ǰ�ᣬ��ѧ�г�֮Ϊ������
��1������֤����
���������ε�̽���н�����ֽ���֣�ֱ��������б���ϵ����ߵ���б�ߵ�һ�룮���ǵ�ʱ��δ˵��������۵ĺ�������������ѧЩ�˾��ε��ж�������֮�Ϳ��Խ����������ˣ���ͼ1����Rt��ABC��CD��б��AB�����ߣ��� �������þ��ε�����˵�������������˵����
�������þ��ε�����˵�������������˵����
��2��Ǩ�����ã������������۽���������⣺
����ͼ2��ʾ���ı���ABCD�У���BAD=90�㣬��DCB=90�㣬EF�ֱ���BD��AC���е㣬����˵��EF��AC��λ�ù�ϵ��
����ͼ3��ʾ��?ABCD�У���ACΪб����Rt��ACE����AEC=90�㣬�ҡ�BED=90�㣬��˵��ƽ���ı���ABCD�Ǿ��Σ�
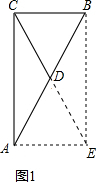 ֤������1����ͼ���ӳ�CD����E��ʹCD=DE������AE��BE��
֤������1����ͼ���ӳ�CD����E��ʹCD=DE������AE��BE����CD=DE����DΪAB�е㣬
���ı���AEBCΪƽ���ı��Σ�
�ߡ�ACB=90�㣬
��ƽ���ı���AEBC�Ǿ��Σ�
��CE=AB��
��CD=
 CE��
CE����CD=
 AB��
AB����2��EF��AC
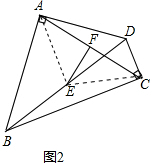 ���������£�
���������£�����AE��CE��
�ߡ�BAD=90�㣬EΪBD�е㣬
��AE=
 DB��
DB���ߡ�DCB=90�㣬
��CE=
 BD��
BD����AE=CE��
��F��AC�е㣬
��EF��AC��
��3������EO��
���ı���ABCDΪƽ���ı��Σ�
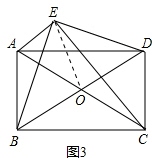
��O��ΪAC��BD�е㣬
�ߡ�AEC=90�㣬OΪAC�е㣬
��
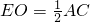 ��
���ߡ�BED=90�㣬OΪBD�е㣬
��
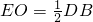 ��
����AC=BD��
��ƽ���ı���ABCD�У�AC=BD��
���ı���ABCD�Ǿ��Σ�
��������1���ӳ�CD����E��ʹCD=DE������AE��BE��Ȼ��֤���ı���AEBC�Ǿ��Σ��ٸ��ݾ��ε����ʿɵ�CD=
 AB��
AB����2��EF��AC������AE��CE��Ȼ����ݣ�1���еĽ��۵õ�AE=CE���ٸ��ݵ��������ε����ʿɵ�EF��AC��
��3������EO�����ݣ�1���еĽ��ۿɵ�OE=
 DB��OE=
DB��OE= AC�������õ�AC=BD�����ݶԽ�����ȵ�ƽ���ı����Ǿ��οɵý��ۣ�
AC�������õ�AC=BD�����ݶԽ�����ȵ�ƽ���ı����Ǿ��οɵý��ۣ�������������Ҫ�����˾��ε��ж������ʣ��ؼ������վ��εĶԽ�������һ���ƽ�֣�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 �������ƶ�����ѧ�γ̱���Ҫ��Ŀγ�Ŀ��֮һ��ͨ����ѧѧϰ��ѧ���ܹ�������ѧ��������ѧ��˼ά��ʽȥ�۲졢������ʵ��ᣬȥ����ճ������к�����ѧ��ѧϰ�е����⣬��ǿӦ����ѧ����ʶ����
�������ƶ�����ѧ�γ̱���Ҫ��Ŀγ�Ŀ��֮һ��ͨ����ѧѧϰ��ѧ���ܹ�������ѧ��������ѧ��˼ά��ʽȥ�۲졢������ʵ��ᣬȥ����ճ������к�����ѧ��ѧϰ�е����⣬��ǿӦ����ѧ����ʶ����
 �������ƶ�����ѧ�γ̱���Ҫ��Ŀγ�Ŀ��֮һ��ͨ����ѧѧϰ��ѧ���ܹ�������ѧ��������ѧ��˼ά��ʽȥ�۲졢������ʵ��ᣬȥ����ճ������к�����ѧ��ѧϰ�е����⣬��ǿӦ����ѧ����ʶ����
�������ƶ�����ѧ�γ̱���Ҫ��Ŀγ�Ŀ��֮һ��ͨ����ѧѧϰ��ѧ���ܹ�������ѧ��������ѧ��˼ά��ʽȥ�۲졢������ʵ��ᣬȥ����ճ������к�����ѧ��ѧϰ�е����⣬��ǿӦ����ѧ����ʶ����