题目内容
甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系 的图象如图.根据图象解决下列问题:
的图象如图.根据图象解决下列问题:(1)
(2)在什么时间段内,两人均行驶在途中(不包括起点和终点),在这一时间段内,请你根据下列情形填空:
当
当
当
(3)分别求出甲、乙两人的行驶速度.
分析:(1)横轴代表时间,甲的时间从0开始,乙的时间从10开始,说明甲先出发,先出发10-0=10分;y轴表示路程,乙在25分时到达终点,甲在30分时到达终点,所以是乙先到终点,先到30-25=5分;
(2)由图中交点可以看出,两人是在20分时相遇.当20分以前时,甲在乙前面;20分以后时,甲在乙后面;
(3)甲行驶速度=6÷甲的行驶时间;乙行驶速度=6÷乙的行驶时间.
(2)由图中交点可以看出,两人是在20分时相遇.当20分以前时,甲在乙前面;20分以后时,甲在乙后面;
(3)甲行驶速度=6÷甲的行驶时间;乙行驶速度=6÷乙的行驶时间.
解答:解:(1)甲的时间从0开始,乙的时间从10开始,说明甲先出发,先出发10-0=10分;y轴表示路程,乙在25分时到达终点,甲在30分时到达终点,所以是乙先到终点,先到30-25=5分.
故填:甲;10分钟;乙;5分钟.(4分);
(2)根据题意,当20分以前时,甲在乙前面;20分以后时,甲在乙后面
故填:10<x<20,x=20,20<x<25(3分);
(3)根据图象用路程除以时间即得:甲的速度为每分钟6÷30=0.2公里,乙的速度为每分钟
=0.4公里.(2分)
故填:甲;10分钟;乙;5分钟.(4分);
(2)根据题意,当20分以前时,甲在乙前面;20分以后时,甲在乙后面
故填:10<x<20,x=20,20<x<25(3分);
(3)根据图象用路程除以时间即得:甲的速度为每分钟6÷30=0.2公里,乙的速度为每分钟
| 6 |
| 25-10 |
点评:本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,能够通过图象得到函数问题的相应解决.注意利用两图象的交点解决问题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 甲骑自行车、乙骑摩托沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图所示.根据图象可知:
甲骑自行车、乙骑摩托沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图所示.根据图象可知: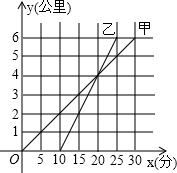 甲骑自行车、乙骑摩托沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图所示.根据图象可知:
甲骑自行车、乙骑摩托沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图所示.根据图象可知: